Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 7

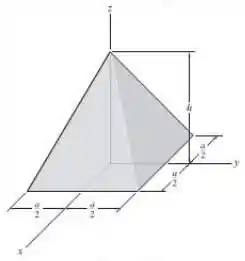
Determine o momento de inércia da pirâmide homogênea de massa m em relação ao eixo z . A densidade do material é ρ . Sugestão: utilize um elemento de placa retangular tendo um volume d V = 2 x 2 y d z .

Passo 1

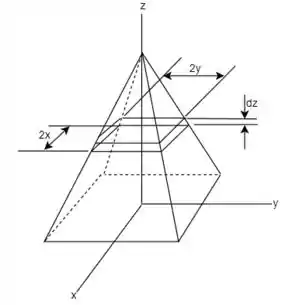
Assim como dito no enunciado do problema, uma das formas para se determinar o momento de inércia seria usando um elemento infinitesimal. Como a base da pirâmide é quadrada, pode-se considerar um elemento infinitesimal de altura d z na forma de uma placa como mostrado no esboço abaixo:

Passo 2

A partir disso, como o exercício pede o momento de inércia em relação ao eixo z , utilizando o valor tabelado do momento de inércia para uma placa fina tem-se:

I z = 1 12 m a 2 + b 2

Onde a e b são os lados dessa placa. Para este caso em particular:

a = b = 2 x = 2 y

Passo 3

Então, derivando ambos os lados da equação do momento de inércia em z obtém-se:

d I z = 1 12 d m 2 y 2 + 2 y 2

Lembrando que d V = ρ d m , consequentemente d m = d V ρ .

Logo:

d I z = 1 12 d V ρ 2 2 y 2 = 8 12 y 2 d V ρ

d I z = 2 3 y 2 d V ρ

Como d V = 2 x 2 y d z = 4 y 2 d z , tem-se:

d I z = 2 3 y 2 ρ 4 y 2 d z = 8 3 ρ y 4 d z

Agora, fazendo o DCL de um triângulo formado pela pirâmide no plano y z :

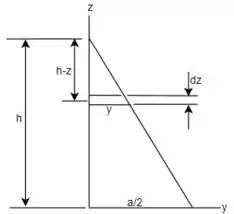
Pode-se aplicar a semelhança de triângulos para se obter:

y h - z = a 2 h ∴ y = h - z a 2 h

Essa expressão para y pode ser substituída na equação encontrada anteriormente, tal que:

d I z = 8 3 ρ h - z a 2 h 4 d z

d I z = ρ 8 3 h - z 4 a 4 h 4 1 16 d z = ρ 6 h - z 4   a h 4 d z

Passo 4

Em seguida, podemos integrar a equação em ambos os lados para se obter o momento de inércia em z :

I z = ρ 6 a h 4 ∫ 0 h h - z 4 d z = ρ 6 a h 4 ∫ 0 h h 4 - 4 h 3 z + 6 h 2 z 2 - 4 h z 3 + z 4 d z

Então, o resultado da integral é:

I z = ρ 6 a h 4 h 5 - 2 h 5 + 2 h 5 - h 5 + h 5 5 = ρ 30 a 4 h

Passo 5

Aproveitando os valores de d m e d V que são dados por:

d m = d V ρ

E:

d V = 2 x 2 y d z = 4 y 2 d z

Então:

d m = 4 y 2 ρ d z

Integrando esta equação:

m = 4 ρ ∫ 0 h h - z a 2 h 2 d z = 4 ρ ∫ 0 h h - z 2 a ² 4 h ² d z

m = ρ a 2 h 2 ∫ 0 h h 2 - 2 h z + z 2 d z = ρ a 2 h 2 h 3 - h 3 + 1 3 h 3

m = ρ a 2 h 3

Observando a última expressão do momento de inércia obtida, ela pode ser reescrita como:

I z = ρ a 2 h 3 a 2 10 ∴ I z = m a 2 10

Resposta

I z = m a 2 10

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando o mecanismo de içamento está operando, a carga de 2000N é submetida a uma aceleração para cima de 1,5 m/s2. Determine a força compressiva que a carga cria em cada uma das colunas, AB e CD. Qual
Se o anel grande, o anel pequeno e cada um dos arcos têm uma massa de 50kg, 7,5kg e 10kg, respectivamente, determine o momento de inércia de massa da roda em relação a um eixo perpendicular à página e
Determine o momento de inércia da massa do pêndulo em relação a um eixo perpendicular à página e passando pelo ponto O . A barra fina tem uma massa de 10kg e a esfera tem uma massa de 15kg.
Determine o momento de inércia do conjunto de aço sólido em relação ao eixo x . O aço tem um peso específico γ = 80 KN/m3.
Determine o momento de inércia da manivela central em relação ao eixo x . O material é aço, com um peso específico γ s t = 80 KN/m3.