Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 53
O aro da roda de tem um raio médio de . Os três raios estão espaçados de um do outro, e cada raio é uma haste uniforme de cujo comprimeno pode ser considerado como sendo de . Se um torque de é aplicado à roda por meio de seu eixo vertical em , calcule a componente horizontal da reação no mancal em quando a roda inicia o movimento a partir do repouso. Despreze a massa do cubo.
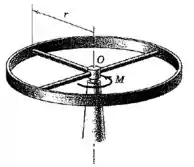
Passo 1
Vamos começar calculando o momento de inércia do conjunto aro-hastes em relação a um eixo que passa pelo ponto :
E podemos consultar as fórmulas para os momentos de inércia do lado direito em uma tabela:
Passo 2
Agora podemos calcular a aceleração angular gerada por um momento de :
Passo 3
E como calcular a componente horizontal da força no mancal em ? Essa componente horizontal é a única força agindo na direçao tangencial do movimento, então pela segunda lei de Newton:
Para encontrar a reação horizontal total no mancal, podemos sem aplicar essa equação a apenas uma das hastes, de forma que a aceleração do centro de massa será:
Então:
Resposta
A força de reação no mancal é .