Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 113
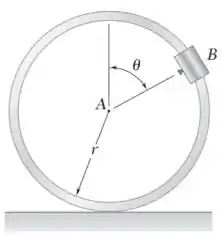
Uma pequena braçadeira de massa mB está presa em B a um arco de massa mh. O sistema é liberado a partir do repouso quando 90° e rola sem deslizar. Sabendo que mh = 3mB, determine (a) a aceleração angular do arco, (b) os componentes horizontal e vertical da aceleração de B.
Passo 1
Cinematica:
Cinética:
Passo 2
(a)Aceleração Angular.
Passo 3
(b)Componentes da aceleração de B.
Resposta
Exercícios de Livros Relacionados
A chapa de aço uniforme de 20k g é livremente articulada em torno do eixo z como mostrado. Calcule a força suportada por cada um dos mancais em A e B imediatamente após a chapa ser liberada a partir d
A metade de um anel de massa m e raio r está soldada a um pequeno eixo horizontal montado em um mancal conforme apresentado. Despreze a massa do eixo e determine a aceleração angular do anel quando um
A barra esbelta de 750m m possui uma massa de 9k g e está montada em um eixo vertical que passsa por O . Se um torque M = 10N m é aplicado à barra por meio de seu eixo, calcule a força horizontal R no
O cilindro maciço homogêneo tem uma massa de 150k g e está livre para girar em torno do eixo horizontal O - O . Se o cilindro, inicialmente em repouso, recebe a ação da força de 400N mostrada, calcule
Determine a aceleração angular e a força no mancal em O para (a) o anel fino de massa m , e (b) o disco circular plano de massa m imediatamete apó cada um deles ser liberado a partir do repouso no pla