Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 95
Um arremessador destro de beisebol lança uma bola curva inicialmente destinada ao canto direito da base principal . Esta faz uma curva de modo a desviar conforme indicado. Assuma que a componente horizontal da velocidade é constante em , despreze o movimento vertical, e estime (a) o raio de curvatura médio da trajetória da bola de beisebol, e (b) a força normal agindo sobre a bola de beisebol de .
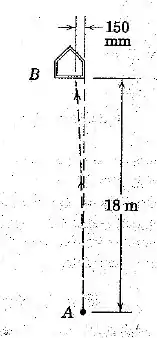
Passo 1
Como queremos calcular o raio de curvartura médio, é interessante construir um triângulo desse jeito:
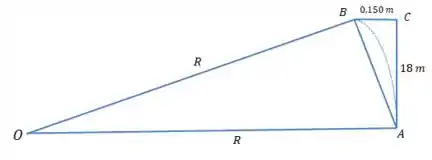
E aí podemos usar a lei dos senos para calcular o raio :
E agora podemos usar alguns truques geométricos para achar esses ângulos e segmentos.
Pelo teorema de pitágoras:
Passo 2
Podemos usar as medidas que já temos para encontrar o ângulo :
E o ângulo é o complementar desse:
E como o triângulo é isósceles, o ângulo é igual a esse:
E como a soma dos ângulos internos do triângulo precisa ser , podemos calcular :
Perceba que o nossa desenho está bem fora de escala.
Passo 3
Então já podemos completar nossa equação de antes:
E agora para encontrar a força normal que age sobre a bola é só usar a fórmula da força centrípeta:
Resposta
e .