Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 66
A árvore jovem, originalmente dobrada, foi trazida para a posição vertical ajustando as três tensões do arame para , e . Determine as reações de força e momento no ponto base do tronco . Negligencie o peso da árvore.
Passo 1
Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar as reações de força e momento no ponto , que atua como um engaste, em relação aos eixos , e . Vamos começar então fazendo o diagrama de corpo livre para o nosso sistema.
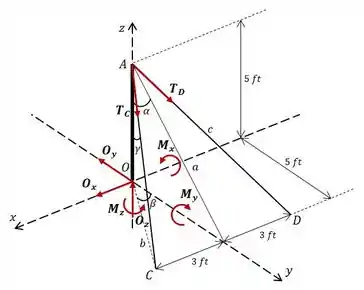
Estranho né? Mas calma que é só a primeira impressão, ao longo dos cálculos você vai ver que fica bem simples! Conforme foi dito no enunciado, as tensões nos cabos são:
Observe que, como , nós não representamos o cabo no diagrama de corpo livre, pois ela é irrelevante para nossos cálculos. Dito isso, o primeiro passo aqui é encontrar algumas medidas que nós definimos no D.C.L.
E, finalmente:
Passo 2
Este é um problema que pode ser facilmente resolvido pelas três equações de equilíbrio de momento (em torno dos eixos , e ) e pelas três equações de equilíbrio de forças, também nas direções dos eixos , e .
Por convenção, vamos adotar que as forças são positivas quando apontam para os sentidos positivo dos eixos e, no caso dos momentos, quando o seu dedão pela regra da mão direita apontar nas direções positivas dos eixos. Então bora começar a trabalhar!
Começando pelas equações de equilíbrio de forças nas direções , e .
Passo 3
Show de bola! Feito isso já temos todas as reações de força do engaste, para descobrir os momentos, vamos usar as equações de equilíbrio de momentos em torno dos eixos , e .
Viu como foi de boa?
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 