Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 69

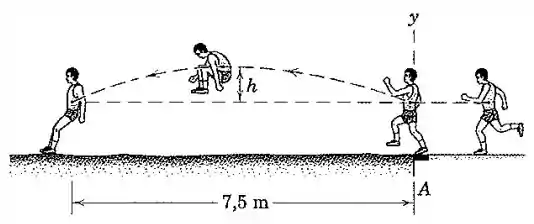
Um atleta de salto em distância atinge a sua tábua de salto A com uma velocidade horizontal de 10   m / s . Determine a componente vertical da velocidade v y do seu centro de gravidade na decolagem para este fazer o salto mostrado. Qual é a ascensão vertical h do seu centro de gravidade?

Passo 1

Pessoal, quando o atleta salta em A , ele tem sua velocidade horizontal v x = 10   m / s e sua velocidade vertical v y , que é o que queremos descobrir primeiro.

O enunciado não faz nenhuma referência a arrasto aerodinâmico, então podemos considerar que a única aceleração quando o atleta está no ar é devido à gravidade, ok? Sendo assim, a velocidade horizontal permanece constante durante todo o processo, e teremos:

v x = x t

t = x v x = 7,5   m 10   m / s = 0,75   s

Ou seja, já descobrimos que o tempo gasto no salto é de 0,75   s .

Passo 2

Como a aceleração vertical a = - g é constante, temos que a velocidade vertical durante o movimento é dada por:

v = v 0 + a t = v y - g t

Porém, quando o atleta atinge sua altura máxima, a velocidade v se anula, e pela simetria do movimento, isso ocorre em t = 0,75 / 2 = 0,375   s :

v = 0 = v y - 9,8   .   0,375

v y = 3,68   m / s

Passo 3

Além disso, devido à aceleração vertical constante, a altura y do centro de massa vai ser dada por:

y = y 0 + v 0 t + 1 2 a t 2

Ou seja,

y = 0 + v y t - 1 2 g t 2 = 3,68 t - 1 2 9,8 t 2

sendo y 0 a altura inicial do centro de massa, considerada como o zero do eixo y .

Quando y = h , al altura máxima, teremos, como já calculamos, t = 0,375   s :

h = 3,68 0,375 - 1 2 9,8 0,375 2

h = 0,69   m

Resposta

v y = 3,68   m / s

h = 0,69   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola é jogada para cima com uma velocidade de 5 m/s do topo de um prédio de 10 m de altura. Um segundo mais tarde, outra bola é jogada verticalmente a partir do chão com uma velocidade de 10 m/s.
Uma partícula move-se ao longo de uma curva definida pela equação s=( t ³-3 t ²+2 t ) ³ ² m, onde t é dado em segundos. Trace os gráficos s - t ,v - t e a - t para a partícula em 0≤t≤3 s .
Um míssil partindo do repouso move-se ao longo de uma pista reta e por 10 s tem uma aceleração, como mostrado. Trace o gráfico v-t que descreve o movimento e descubra a distância percorrida em 10 s.
O obturador mostrado na figura foi formado removendo-se um quarto de um disco de 20 mm de raio e é usado para interromper um feixe de luz emitido a partir de uma lente em C. Sabendo que o obturador te
Agua é esguichada em um ângulo de 90° a partir da inclinação a 20 m/s. Determine o alcance R.