Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.10 - Ex. 222
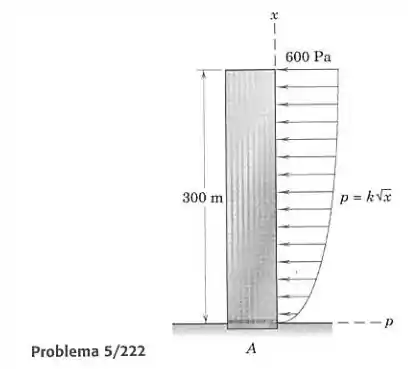
Como parte de um estudo preliminar de um projeto, estão sendo investigados os efeitos das cargas devidas ao vento em um prédio de 300 m. Para a distribuição parabólica da pressão do vento, mostrada na figura, calcule as forças e o momento da reação na base do prédio devido ao carregamento causado pelo vento. A largura do prédio (perpendicular ao papel) vale 60 cm.
Passo 1
Queremos calcular a força causada pelo vento e o momento total que o vento causa em torno da base, que é igual ao momento de reação que impede o giro. Vamos dividir o prédio em elementos infinitesimais retangulares horizontais de altura . A força causada pelo vento em cada elemento desses será , sendo a pressão para a altura do elemento a partir da base e a área dada pela largura do prédio, igual a 60 m, vezes :
Então a força e o momento total causados na base são:
Passo 2
Vamos primeiro obter em função de . A pressão segue a lei . Como :
Então a pressão é:
Passo 3
Vamos obter a força total:
Agora vamos integrar para obter o momento total: