Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 43
O atuador pneumático em é usado para aplicar uma força de sobre o membro em . A reação normal do eixo liso em sobre o membro é de 300 N. Determine a intensidade de e as componentes horizontal e vertical da reação no pino .
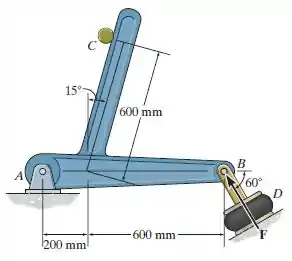
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Como esta questão utiliza a mesma geometria da questão , vamos utilizar as relações lá desenvolvidas para o cálculo das reações aqui nesta nossa questão!
Relembrando, as relações foram:
Estas três equações serão fundamentais para resolvermos o problema.
Aqui, nos foi dado a força . Com esta informação, a questão pede para que calculemos as forças e as componentes e da reação no pino .
Então, vamos as contas!
Passo 2
Esta vai ser uma questão basicamente de aplicação da fórmula. Começamos então calculando a força . Ela será:
Agora, vamos calcular as componentes da reação no pino . Começando por , temos:
Já para , temos:
E assim finalizamos a questão