Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 23
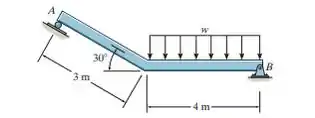
Se o rolete em e o pino em podem suportar uma carga de até e , respectivamente, determine a intensidade máxima da carga distribuída , medida em , de modo que não haja ruptura dos suportes.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Como esta questão utiliza a mesma geometria da questão , vamos utilizar as relações lá desenvolvidas para o cálculo das reações aqui nesta nossa questão!
Relembrando, as relações foram:
Percebam que as reações no pino são funções da reação no rolete . E que a força no rolete é função apenas do carregamento .
A questão nos afirmou que os valores máximos nas reações dos apoios são:
Então, temos duas possibilidades: a reação em é máxima, e a reação no apoio será menor que ; ou a reação no apoio é máxima, e a reação é menor que .
Sendo assim, vamos testar qual hipótese está correta!
Passo 2
Vamos começar com a primeira hipótese, que . Desta forma, a força devido ao carregamento é:
E com isto, as reações no pino são:
E então, a intensidade da força no pino , temos:
E como , acabamos de verificar que a nossa primeira hipótese está errada!
Passo 3
Como a nossa primeira hipótese está errada, é bastante provável que a nossa segunda esteja correta. As contas serão um pouco mais trabalhosas, mas nada impossível!!!
Então, vamos confirmar ela agora! Neste caso, temos . Logo,
Só que nós sabemos que:
Portanto,
E conseguimos um valor de . Portanto, a nossa segunda hipótese está válida!
Seguindo com as contas, obtemos . Mas como queremos determinar o carregamento distribuído , temos:
E assim finalizamos a questão!