Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.6 - Ex. 46

O disco circular está girando em torno de seu próprio eixo (eixo y) à taxa constatne de ρ = 10 π   r a d / s . Simultaneamente, aestrutura está girando em torno do eixo Z à taxa constante Ω = 4 π   r a d / s . Calcule a aceleração angular α do disco e a aceleração do Ponto A na parte mais alta do disco. Os eixos x-y-z estão associados à estrutura, que possui a orientação instantânea mostrada, com respeito aos eixos fixos X-Y-Z.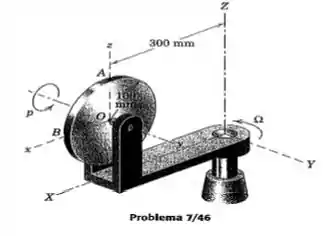

Passo 1

Ω= 4 * π r a d s 2 ρ = 10 * π r a d s 2 r 0 = 300   I   m m = 0,3   m r 0 a = 100   m m   K   =0,1 K m

Onde I e K são as direções dos raios

Informações importantes para a resolução do problema.

Passo 2

O disco está girando a uma taxa constante ρ   no eixo y e a uma taxa constante Ω   no eixo Z, utilizando a regra da mão direita podemos determinar o sentido dos vetores velocidade angular para cada um dos giros, assim temos   ρ =   ρ * j e   Ω = Ω * K portanto a aceleração angular( α   ) do disco será α = ρ × Ω equação (7/3).

α = i j k 0 ρ 0 0 0 Ω = - ρ * Ω * i = - 10 * π * 4 * π * i = - 40 π 2 * i r a d s 2

Passo 3

Podemos agora calcular a aceleração linear no ponto A utilizando a equação 7/6

a A = a b + Ω ˙ × r b a + Ω × Ω × r b a + 2 * Ω × v r e l + a r e l

Chamaremos a b   d e   a 0 a aceleração devida à o raio   r 0

e r b a   d e   r 0 a que é a distância do disco até a origem de X-Y-Z

a 0 = Ω × Ω × r 0 = Ω × i j k 0.3 0 0 0 0 Ω = Ω × ( 0.3 * Ω   j )

a 0 = i j k 0 0.3 Ω 0 0 0 Ω = - 0.3 Ω 2 * i = - 0.3 * 4 * π 2 2 * i = - 4.8 π 2 * i m s 2

Como Ω é uma constante sua derivada Ω ˙ será zero e por consequência Ω ˙ × r b a = 0

v r e l =   ρ × r 0 a = i j k 0 ρ 0 0 0 0.10 = - ρ * 0.1 * i = 10 π * 0.1 * i = π * i m s

2 * Ω × v r e l = 2 * i j k 0 0 Ω π 0 0 = 2 * Ω * π * j = 2 * 4 * π 2 * j = 8 * π 2 * j

a r e l = ρ × ρ × r 0 a = - 10 * π 2 * k

Portanto a A = - 4.8 π 2 * i +   8 * π 2 * j +   - 10 * π 2 * k m s 2

Resposta

a A = - 4.8 π 2 * i +   8 * π 2 * j +   - 10 * π 2 * k m s 2

α = - 40 π 2 * i r a d s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

106. As pás e o cubo do rotor do helicóptero têm uma massa de 64k g e um raio de giração de 3,0m em relação ao eixo de rotação z . Com o rotor girando a 500r p m durante um curto intervalo após a deco
98. A estudante se ofereceu voluntariamente para auxiliar em uma demonstração na sala de aula envolvendo uma roda com quantidade de movimento, que está girando rapidamente com velocidade angular p com
102. Um ônibus ecológico experimental é acionado pela energia cinética armazenada em um grande volante que gira a uma alta velocidade p no sentido indicado. Quando o ônibus encontra uma pequena rampa
101. Um aeroplano acaba de deixar a pista com uma velocidade de decolagem v . Cada uma de suas rodas que gira livremente possui uma massa m , com um raio de giração k em relação ao seu eixo. Quando ob
A carcaça de um motor elétrico é livremente articulado em torno do eixo horizontal x, que passa através do centro de massa G do rotor. Se o motor está girando a taxa constante de ϕ ˙ = p , determine a