Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 126
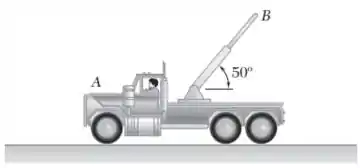
À medida que o caminhão mostrado na figura começa a dar ré com uma aceleração constante de 1,2 m/s² , a seção exterior B da sua lança começa a se retrair com uma aceleração constante de 0,5 m/s² relativa ao caminhão. Determine (a) a aceleração da seção B e (b) a velocidade da seção B quando t=2 s.
Passo 1
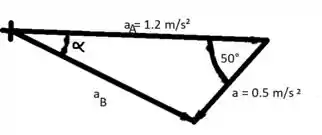(a)Nós temos
A representação gráfica dessa equação é como mostrada.
Nós temos
ou
e
ou
Passo 2
(b)Para o movimento de aceleração uniforme
Em t=2s
ou
Resposta
Exercícios de Livros Relacionados
Uma cápsula impulsionada a vácuo para um sistema de transporte tubular de alta velocidade do futuro está sendo projetada para operação entre duas estações A e B , que estão distantes 10k m . Se a acel
A resistência aerodinâmica ao movimento de um carro é aproximadamente proporcional ao quadrado da sua velocidade. A resistência adicional ao atrito é constante, de modo que a aceleração do carro quand
Um velocista atinge sua velocidade máxima v m á x á em 2,5 segundos partindo do repouso com aceleração constante. Mantém então esta velocidade e termina 100 metros no tempo total de 10,40 segundos. De
O corpo caindo com velocidade v 0 colide e mantém contato com a plataforma apoiada por um jogo de molas. A aceleração do corpo após o impacto é a = g - c y , onde c é uma constante positiva e y é medi
O movimento horizontal do êmbolo e do eixo é dificultado pela resistência ao movimento do disco através do banho de óleo. Se a velocidade do êmbolo é v 0 na posição A onde x = 0 e t = 0 , e se a desac