Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 76

Um avião a jato de 16 Mg mantém uma velocidade constante de 774 km/h enquanto sobe com um ângulo de rampa de α = 18°. A aeronave admite ar a uma razão de 300 kg/s e o descarrega com uma velocidade de 665 m/s em relação à aeronave. Se o piloto muda para um voo horizontal enquanto mantém o mesmo ajuste de motor, determine (a) a aceleração inicial do avião, (b) a velocidade horizontal máxima obtida. Considere que o arrasto devido ao atrito com o ar é proporcional ao quadrado da velocidade.

Passo 1

Vamos então resolver mais essa. Aqui temos todo o movimento de subida e aceleração de um avião a jato. Vamos ver a disposição das forças na figura abaixo:

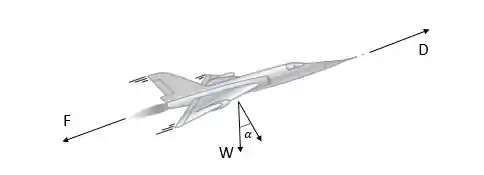
Quando o avião está subindo, a velocidade é constante. Logo:

F - D - m g sin ⁡ α = 0

F - D = 16000 ⋅ 9,81 ⋅ sin ⁡ 18 ° = 48454   N

Quando a aeronave fica na horizontal, em movimento acelerado, temos:

F - D = m a

16000 a = 48454

a = 3,03   m / s 2

Passo 2

A força de arrasto da aeronave pode ser calculada como:

D = k v 1 2

E a força de tração do motor pode ser expressa como:

F = d m d t ( v 2 - v 1 )

Assim, podemos calcular o coeficiente de arrasto no momento da aceleração inicial da aeronave após a subida:

d m d t v 2 - v 1 - k v 1 2 = 48454

k = 300 665 - 774 ÷ 3,6 774 ÷ 3,6 2

k = 1,872   N ⋅ s 2 / m 2

Passo 3

Assim, a velocidade máxima do avião em voo horizontal, quando a velocidade volta a ser constante:

F - D = 0

d m d t v 2 - v 1 - k v 1 2 = 0

k v 1 2 + d m d t v 1 - d m d t v 2 = 0

1,872 v 1 2 + 300 v 1 - 199500 = 0

v 1 = 256 m / s = 922   k m / h  

Resposta

  1. 3,03 m/s²
  2. 922 km/h
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um sistema consiste de três partículas,A,BeC. Sabemos quemA= 3 kg,mB= 4 kg emC= 5 kg e que as velocidades das partículas, expressas em m/s são, respectivamente,vA= − 4i+ 4j+ 6k,vB= − 6i+ 8j+ 4kevC= 2i
Um vagãoAde massa de 45.000 kg move-se em um pátio de manobras ferroviário com uma velocidade de 10 km/h em direção aos vagõesBeC, ambos em repouso com os freios liberados e a curta distância um do ou
Um homem de 90 kg e uma mulher de 60 kg estão lado a lado na mesma extremidade de um barco de 150 kg, prontos para mergulhar, cada um com uma velocidade de 5 m/s em relação ao barco. Determine a veloc
Um sistema consiste de três partículas,A,BeC. Sabemos quemA= 3 kg,mB= 4 kg emC= 5 kg e que as velocidades das partículas, expressas em m/s, são respectivamente,vA= − 4i+ 4j+ 6k,vB=vxi+vyj+ 4kevC= 2i−
Em um parque de diversões há carros bate-bateA,BeCde 200 kg com pilotos com massas de 40 kg, 60 kg e 35 kg respectivamente. O carroAestá se movendo para a direita com a velocidadevA= 2 m/s e o carroCt