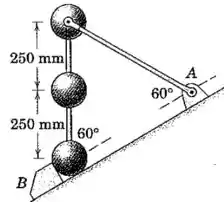
As três esferas idênticas, cada uma de massa , estão apoiadas no plano vertical sobre o plano inclinado de . As esferas estão soldadas às duas hastes de conexão de massa desprezível. A haste superior, também de massa desprezível, é livremente articulada à esfera superior e ao suporte em . Se o obstáculo em é repentinamente removido, determine a velocidade com que a esfera superior atinge o plano inclinado. (Observe que a velocidade correspondente à esfera do meio é .) Explique a perda de energia que ocorreu após todo o movimento cessar.
Passo 1
Pelo desenho podemos ver que as duas hastes e o plano formam um triângulo, e como os três ângulos internos são iguais a podemos garantir que é um triângulo equlátero, e então o comprimento da haste apoiada em é:
Vamos resolver essa questão pensando em energia mecânica, então precisamos começar calculando qual foi a queda vertical total de cada uma das esferas:
Antes a situação era a seguinte:
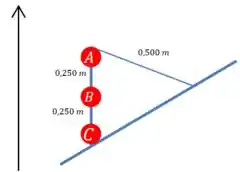
E depois da queda:
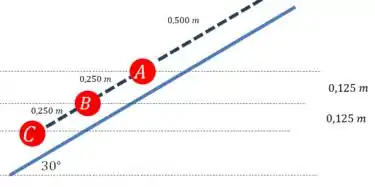
E os deslocamentos verticais foram:
Passo 2
E então a variação total da energia potencial gravitacional do sistema é:
E a variação da energia cinética é mais fácil de calcular, considerando que a velocidade inicial de todos é zero e que as velocidades finais de cada bola são:
E então:
Passo 3
Agora vamos aplicar a lei de conservação da energia mecânica:
Nesse caso nós analisamos a variação entre dois instantes: desde quando todo o sistema ainda estava em repouso, até o momento imediatamente antes da queda.
Logo após a colisão é de se esperar que todo o movimento vai cessar, e isso quer dizer que a energia mecânica total já não é a mesma de antes. Isso quer dizer que ouve perda de energia durante a colisão, associado ao impacto das bolas contra o plano inclinado.
Resposta
A velocidade com que a esfera superior atinge o plano inclinado é . A perda de energia está associada ao impacto das bolas contra o plano.