Se o motor M exerce uma forca sobre o cabo, onde é dado em segundos, determine a velocidade da caixa de quando . Os coeficientes de atrito estático e cinético entre a caixa e o plano são , respectivamente. A caixa está inicialmente em repolso.

Passo 1
A primeira etapa da solução do problema é sabermos se a força é suficiente para mover a caixa, visto que, se esta força for menor que a força de atrito estático, , a caixa não se moverá. Então, pelo diagrama de corpo livre, temos:
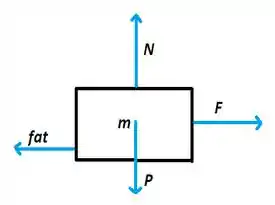
Aplicando a Segunda Lei de Newton na direção ,
N
Por definição,
N
Comparando com o valor de ,
Logo, há movimento, pois a força de atrito estática não consegue ser igual à .
Passo 2
Agora que sabemos que provocará um movimento na caixa, devemos aplicar a segunda lei de Newton na direção onde há movimento, e então obter uma equação para a aceleração, em função do tempo, :
Passo 3
Sabendo que,
Agora é só integrar,
Passo 4
Resolvendo para segundos,
m/s
Resposta
A velocidade no instante segundos é m/s.