Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 159
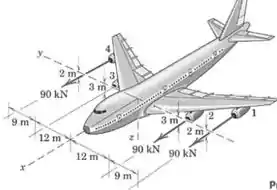
O avião de passageiros do problema está redesenhado aqui com informações tridimentionais. Se a turbina falha subitamente, determine a resultante dos vetores de empuxo das três turbinas remanescentes, cada um tendo módulo de . Especifique as coordenadas e do ponto pelo qual passa a linha de ação da resultante. Esta informação seria crítica para os critérios de projeto de desempenho sob falha de uma turbina.
Passo 1
Vamos começar calculando a força resultante. As três forças (das turbinas , e ) agem na direção do eixo e têm o mesmo módulo, então:
Passo 2
Agora vamos analisar os momentos das forças. Como elas são paralelas ao eixo , elas produzem momento em torno dos eixos e .
Começamos calculando o momento em torno do eixo . Nesse caso todas as forças favorecem a rotação no mesmo sentido:
E para o momento em torno do eixo , a força que está “sozinha” na esquerda favorece a rotação no sentido oposto às outras duas:
Passo 3
Mas nosso objetivo é encontrar as coordenadas e em que a força resultante age. Nesse caso temos que escolher essas coordenadas de forma que o momento resultante seja o mesmo que calculamos acima.
Em torno do eixo temos a seguinte igualdade:
E em torno do eixo :
Mas é preciso corrigir o sinal. Para que a rotação gerada pela força resultante seja a mesma que seria gerada pelas três forças que estão na figura, a força tem que ser aplicada na asa esquerda do avião, que está no lado negativo do eixo :
Resposta
As coordenadas devem ser e .