Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 124
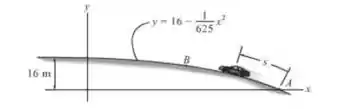
Se o carro passa o ponto A com uma velocidade escalar de e começa a aumentar sua velocidade escalar a uma razão constante de , determine a intensidade da aceleração do carro quando .
Passo 1
Precisamos determinar a intensidade da aceleração. Como já nos foi dado a sua componente tangencial, só precisamos calcular a sua componente normal. Mas aí a gente se questiona: e cadê o raio de curvatura? Este é o ponto mais difícil da questão. Para calcularmos o raio de curvatura, será necessário utilizarmos a seguinte equação:
A questão agora é: qual o valor de ? Como sabemos que , temos que para a função dada. Portanto, a coordenada é 0, ele está na origem (partiu de A, em ). Agora, é só calcularmos como sempre fizemos!
Passo 2
Como a aceleração tangencial é constante, calcularemos a velocidade através da seguinte fórmula:
Agora que temos a velocidade, já conseguimos calcular a componente normal da aceleração.
Passo 3
Antes de calcularmos a componente normal, precisamos determinar o raio de curvatura. Para isto, utilizaremos a fórmula do Passo 1. Primeiramente, derivaremos a função que governa a nossa curva duas vezes. Sendo assim:
Substituindo na fórmula do raio de curvatura, temos:
Quando , temos:
Passo 4
Calculando a componente normal, temos:
Portanto, a intensidade da aceleração é: