Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 33

O bloco B de massa 10 kg repousa na superfície superior de uma cunha de 22 kg como mostra na figura. Sabendo que o sistema é liberado do repouso e desprezando o atrito, determine (a) a aceleração de B, (b) a velocidade de B em relação a A em t = 0,5 s.

Passo 1

E ai gurizada tudo certinho? O enunciado pede que a gente determine a aceleração de B, (b) a velocidade de B em relação a A em t = 0,5 s. Vamos realizar um esboço primeiramente do elemento em A, vem comigo >D

A:

  1. + ↙ Σ F x = m A a A :       W A sin ⁡ 30 ° + N A B cos ⁡ 40 ° = m A a A

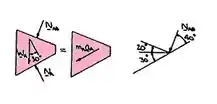
    ou

    N A B = 22 a A - 1 2 g cos ⁡ 40 °

    Agora notamos: aB = aA + aB/A, onde aB/A é direcionado ao longo da superfície superior de A.

    Passo 2

    Agora vamos considerar apenas em B

    B:

    + ↗ Σ F y ´ = m B a y ´ :         N A B - W B cos ⁡ 20 ° = - m B a A sin ⁡ 50 °

    ou

    N A B = 10 g cos ⁡ 20 ° - a A sin ⁡ 50 °

    Equacionando as duas expressões para NAB

    22 a A - 1 2 g cos ⁡ 40 ° = 10 g cos ⁡ 20 ° - a A sin ⁡ 50 °

    ou

    a A = 9.81 1.1 + cos ⁡ 20 ° cos ⁡ 40 ° 2.2 + cos ⁡ 40 ° sin ⁡ 50 ° = 6.4061   m/ s 2

    + ↘ Σ F x ´ = m B a x ´ :       W B sin ⁡ 20 ° = m B a B / A - m B a A cos ⁡ 50 °

    ou

    a B / A = g sin ⁡ 20 ° + a A cos ⁡ 50 ° = 9.81 sin ⁡ 20 ° + 6.406 cos ⁡ 50 ° m/s 2 = 7.4730   m/s 2

    Passo 3

    Finalmente podemos somar as acelerações com os valores que obtivemos até então :D

    a B = a A + a B / A

    Nós temos

    a B 2 = 6.4061 2 + 7.4730 2 - 2 6.4061 × 7.4730 cos ⁡ 50 °

    ou

    a B = 5.9447   m/s 2

    e

    7.4730 sin ⁡ α = 5.9447 sin ⁡ 50 °

    ou

    α = 74.4 °

    Passo 4

  2. Nota: Temos movimento uniformemente acelerado, de modo que

v = 0 + a t

Agora

v B / A = v B - v A = a B t - a A t = a B / A t

Em t = 0.5 s basta substituirmos e fim, ufa!!

v B / A = 7.4730   m/ s 2 × 0,5  s = 3,74   m / s

Resposta

a)  a B = 5.94   m/ s 2 75.6 °

b)  v B / A = 3.74   m/s 20 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O sistema de três partículas possui as massas, velocidades e forças externas indicadas nas partículas. Determine r - , r - ˙ , r - ¨ , T , H O e H O ˙ para esse sistema.
Os três vagões de carga estão se deslocando ao longo do trilho horizontal com as velocidades indicadas. Após os impactos ocorrerem, os três vagões se tornam acoplados e se movem com uma velocidade com
O homem de massa m 1 e a mulher de massa m 2 estão em pé sobre extremos opostos da plataforma de massa m 0 que se desloca com atrito desprezível e está inicialmente em repouso com s = 0 . O homem e a
A mulher A de 60k g , o capitão B de 90k g , e o marinheiro C de 80k g estão sentados no barco de 150k g , que está deslizando através da água com uma velocidade de 1 nó. Se as três pessoas mudam suas
As três pequenas esferas de aço, cada uma com massa de 2,75k g , estão unidas pelas conexões articuladas de massa desprezível e comprimentos iguais. As esferas são liberadas a partir do repouso nas po