Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 6.Problemas - Ex. 106
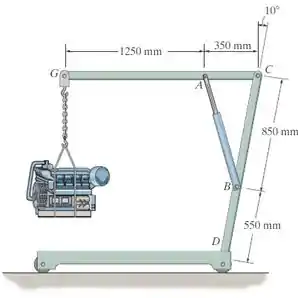
O guincho é usado para suspender o motor de . Determine a força que atua no cilindro hidráulico , as componentes horiozntal e vertical da força no pino e as reações no apoio fixo .
Passo 1
Vamos olhar primeiro para o triângulo :
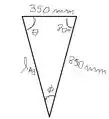
Para encontrarmos o valor de podemos aplicar a lei dos cossenos! Assim,
Para agora encontrar o valor do ângulo , podemos usar a lei dos senos! Logo,
Passo 2
Para um corpo em equilíbrio, o somatório dos momentos em relação em um ponto é igual a zero.
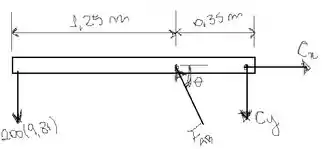
Assim, calculando o momento em relação ao ponto e adotando como sentido positivo o anti-horário, temos:
Além do momento, o somatório de forças nos eixos de referência ( para um corpo em equilíbrio também deve ser igual a zero. Assim, assumindo como direção positiva para cima e para direita, temos:
Passo 3
Vamos olhar para o diagrama de corpo livre do guincho:
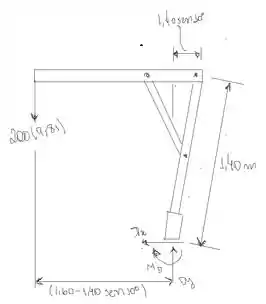
O somatório de forças nos eixos de referência ( para um corpo em equilíbrio também deve ser igual a zero. Assim, assumindo como direção positiva para cima e para direita, temos:
Para um corpo em equilíbrio, o somatório dos momentos em relação em um ponto é igual a zero. Assim, calculando o momento em relação ao ponto D e adotando como sentido positivo o anti-horário, temos:
Resposta
As forças são: