Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 29
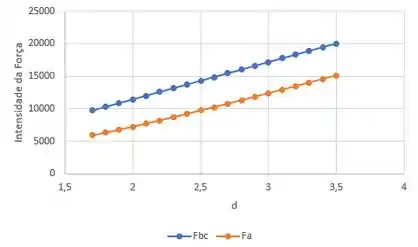
5.29. A massa de é suspensa por um gancho que se move ao longo de um trilho até . Determine a força ao longo da cantoneira conectada por pino BC (ligação curta) e a intensidade da força no pino A como uma função da posição . Represente graficamente esses resultados de e (eixo vertical) em função de (eixo horizontal).
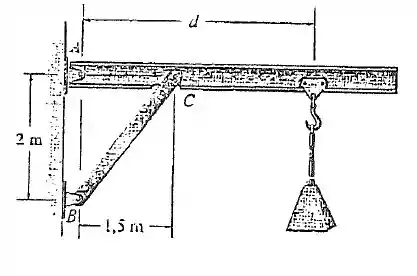
Passo 1
Bem a barra que está no eixo está em equilíbrio, então a soma das forças na barra deve estar em equilíbrio. Vamos fazer o DCL:
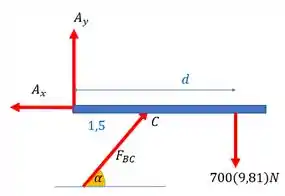
Vamos entender essas variáveis.
- é a força em BC
- é esse ângulo
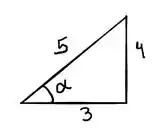
Vemos isso pela figura. O lado é paralelo a medida de m, o de é paralelo a medida de , formando os catetos desse triângulo que desenhamos. Então podemos fazer
- é a distância do pino A até a massa
Com isso em mente, podemos usar as equações de equilíbrio para achar e a força em em função de como ele pede.
Vamos!
Passo 2
Vamos começar calculando o somatório de momentos em que é o ponto com mais reações. A gente vai adotar como sentido positivo o sentido anti-horário. Para fazer esse somatório, somamos todos os termos:
Onde é a distância de até a força. Ficamos assim:
Uma resposta já foi!
Passo 3
Beleza, vamos agora podemos aplicar as condições de equilíbrio no pino A, começando pelo eixo x
Então
Passo 4
Agora para o eixo y
Então
Passo 5
Agora podemos determinar que é a força resultante em A somando as forças em
Passo 6
Agora podemos usar essas equações para construir o gráfico
