Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 27

Determine as forças normal e cortante e o momento fletor nos pontos C e D da viga simplesmente apoiada. O ponto D está localizado logo à esquerda da carga concentrada de 10   k N .

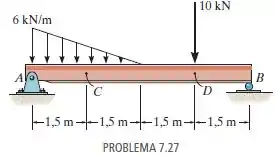
Passo 1

Oi tudo bem? Vamos resolver este exercício.

Queremos as forças normal e cortante e o momento fletor nos pontos C e D .

O primeiro a ser feito é o diagrama de corpo livre do sistema. Temos que:

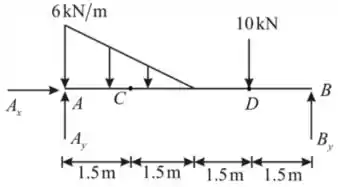
Considerando o momento em A , temos que:

∑ M A = 0

B y 6 - 10 4,5 - 1 2 3 6 1 3 ⋅ 3 = 0

6 B y = 54

B y = 9   k N

Analisando o equilíbrio vertical, temos que:

A y + B y - 1 2 3 6 - 10 = 0

A y = 10   k N

Passo 2

Para descobrir as reações relacionadas ao ponto C , vamos fazer um corte e analisar a seção C B . Temos que:

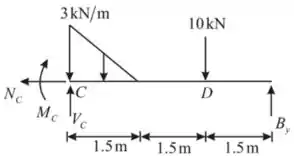
Você deve estar se perguntando o porquê de a carga distribuída estar com valor de 3   k N / m . Encontramos esse valor através da analise de semelhança de triângulos:

6 A E = h C E

6 3 = h 1,5

h = 3   k N / m

Vamos analisar o equilíbrio com relação à direção da normal:

∑ N = 0

N C = 0

Agora analisando o equilíbrio com relação a cortante, temos que:

∑ V = 0

V C - 1 2 3 1,5 - 10 + B y = 0

V C = 1 2 3 1,5 + 10 - 9

Logo:

V C = 3,25   k N

Analisando o equilíbrio com relação ao momento fletor, temos que:

∑ M = 0

M C = B y 4,5 - 10 3 - 1 2 3 1,5 1 3 ⋅ 1,5

M C = 9,375   k N ⋅ m

Passo 3

Vamos fazer a mesma análise, agora para o ponto D . Temos que:

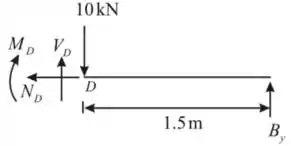
Vamos analisar o equilíbrio com relação à direção da normal:

∑ N = 0

N D = 0

Agora analisando o equilíbrio com relação a cortante, temos que:

∑ V = 0

V D + B y - 10 = 0

V D = - 9 + 10

Logo:

V D = 1   k N

Analisando o equilíbrio com relação ao momento fletor, temos que:

∑ M = 0

M D = B y 1,5

M D = 13,5   k N ⋅ m

Resposta

N C = 0

V C = 3,25   k N

M C = 9,375   k N ⋅ m

N D = 0

V D = 1   k N

M D = 13,5   k N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as forças normal e cortante e o momento fletor nos pontos E e F na viga composta de dois elementos. O ponto F está localizado logo à esquerda da força de 15k N e do momento de binário de 25k
Determine a razão a / b para a qual a força cortante será zero no ponto intermediário C da viga.
Determine os diagramas da força cortante e o momento fletor para a viga.
Uma corrente é suspensa entre pontos na mesma altura e espaçados de uma distância de 60 m. Se tiver uma massa por unidade de comprimento de 8 kg/m e a flecha for 3 m, determine a tração máxima na corr
Determine os diagramas da força cortante e o momento fletor para a viga.