Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas Revisão - Ex. 150

Sabendo-se que o diâmetro da barra de aço A B D é 30   m m , determinar (a) os planos principais; (b) as tensões principais; (c) a máxima tensão de cisalhamento, no ponto H .

Passo 1

Fala aí, galera!! Vamos resolver mais um exercício de resmat? Melhor que ficar bebendo no bar né não? kkkSe liga, primeiro a gente vai pegar esse força de 2   k N e vai fazer ela atuar no centro da seção H . Com isso a gente vai poder desenhar um diagrama de tensões relacionado ao ponto H .

Daí pra frente é receita de bolo pessoal, porque pra achar o ângulo das tensões principais 2 θ p a gente usa uma formulinha:

tan ⁡ 2 θ p = 2 τ x y σ x - σ y

Aí a gente calcula o raio e o centro do ciclo de mohr para achar as tensões principais e com o ciclo vai ficar fácil achar a máxima tensão de cisalhamento em H .

Então partiu beber?

Quer dizer, partiu resolver essa questão iradosa?

Passo 2

Como a gente disse vamos transferir essa força de 2   k N para o ponto H . Ao fazer isso a gente precisa compensar com um momento puro também, então vamos calcular o momento que essa força faz na barra:

M = F × d

Galera, essa força tem direções em y e em x então a gente precisa decompor ela, vai ficar olha:

F x = - 2 c o s ( α )

F y = 2 s e n ⁡ ( α )

Mas quem é α ? α é o ângulo entre a força a hipotenusa E D e o cateto de 150   m m . Pessoal, esse é um triângulo daqueles (3,4,5) mas cada lado ta multiplicado por 50. Então é um triângulo (150, 200, 250).

Assim vamos ter que:

cos ⁡ α = 150 250 = 0,6

s e n α = 200 250 = 0,8

Então a força vai ser:

F x = - 2 × 0,6 = - 1,2   k N

F y = 2 × 0,8 = 1,6   k N

Então a gente pode representar a força como:

F = - 1,2   i ^ + 1,6 j ^ k N

Como a gente quer os momentos então a gente tem que fazer o produto vetorial de um com o outro:

M = F × d

Logo, faz sentido colocar as distâncias do ponto H até o ponto D , onde a força é aplicada, em função dos vetores unitários:

d = 0,225   k ^   ; 0,125   i ^   m

Fazendo o produto vetorial:

M = F × d

M = - 1,2   i ^ + 1,6 j ^ × 0,225   k ^   ; 0,125   i ^

Aqui vamos utilizar os vetores unitários ( i ^ , j ^ , k ^ ) para achar a direção certinha do momento. Você também pode utilizar a regra da mão direita se quiser =D

M = ( 0,36   i ^ ; 0,27   j ^   ; - 0,2   k ^ )

Agora vem uma coisa interessante, os momentos em y e em z são os momentos fletores (irão causar uma flexão e consequentemente uma tensão normal); já o momento em x irá causar uma torção e, consequentemente, uma tensão cisalhante!

Passo 3

Pessoal, agora é só colocar esses momentos em H :

Agora temos de transformar esse desenho num diagrama de tensões:

Para calcular as tensões normais a gente precisa daquela equação que relaciona a tensão normal com o momento:

σ = M   c J

O valor de c sempre será o do raio da nossa barra:

c = 30 2 = 15   m m

E o valor do momento polar de inércia também:

J = π r 4 2

J = π 0,015 4 2 = 7,952 × 10 - 8   m 4

Agora é só substituir os valores:

σ x = M y   c J

Repare que um momento em x gera uma tensão normal em y , porque esse momento tenta esticar a barra A B , por isso é uma tensão normal, além de ser normal é trativa então vamos ter:

σ x = 270 × 0,015 7,952 × 10 - 8 = 50,93   M P a

Para a tensão em y :

σ y = M x   c J

σ y = 36 0 × 0,015 7,952 × 10 - 8 = 67,90   M P a

Agora para a tensão cisalhante τ x y :

τ x y = T   c J

τ x y = - 2 00 × 0,015 7,952 × 10 - 8 = - 37,73   M P a

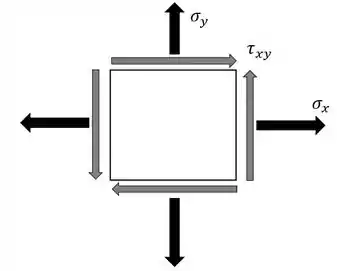
Então o nosso ponto H fica com o seguinte estado de tensões:

Repara que as tensões cisalhantes (cinzas) mudaram de sentido, isso acontece porque a tensão é negativa, beleza?

Passo 4

Agora vamos calcular os planos das tensões principais 2 θ p :

t g 2 θ p = 2 τ x y σ x - σ y

t g 2 θ p = 2 × - 37,73 50,93 - 67,90 = 4,447

2 θ p = a r t g ( 4,447 )

2 θ p = 77,36 °

θ p = 38,66 °

Como a gente tem que pergar o ângulo complementar também..

θ p 2 = 90 - 38,66 = 51,34 °

Passo 5

Agora vamos calcular o centro do circulo de mohr:

σ m é d = σ x + σ y 2

σ m é d = 50,93 + 67,90 2 = 59,42   M P a

E o raio:

R = σ x - σ y 2 2 + τ x y 2

R = 50,93 - 67,90 2 2 + 37,73 2 = 41,37   M P a

Dessa forma as tensões principais são:

σ m á x = σ m é d + R

σ m á x = 59,42 + 41,37 = 100,8   M P a

σ m í n = σ m é d - R

σ m í n = 59,42 - 41,37 = 18,05   M P a

Passo 6

A máxima tensão de cisalhamento é igual ao raio:

τ m á x = R = 41,37   M P a

Resposta

a)

θ p = 38,66 °

θ p 2 = 51,34 °

b)

σ m á x = 100,8   M P a

σ m í n = 18,05   M P a

c)

τ m á x = 41,37   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os elementos AB e BC são feitos de aço (E = 29x10 6 p s i ) e têm seção transversal com área de 0,80i n 2e0,64i n 2 , respectivamente. Para o carregamento mostrado, determine o alongamento do (a) elem
Cada uma das barras AB e CD é feita de alumínio ( E = 10,9x10 6 p s i e tem uma seção transversal com área de 0,2 i n 2 . Sabendo que elas suportam a barra rígida BC, determine o deslocamento do ponto
A barra ABC é feita de um alumínio para o qual E = 70G P a . Sabendo que P = 6 kN e Q = 42k N , determine o deslocamento de (a) ponto A e (b) ponto B.
O tubo de latão AB E = 105G P a tem área de seção transversal de 144 m m 2 e é ajustado com plugue em A. O tubo está conectado em B a uma placa rígida que, por sua vez, está conectada em C ao fundo de
O pórtico de aço ( E = 200G P a ) mostrado tem a escora diagonal BD com área de 1920 m m 2 . Determine a máxima carga P admissível se a mudança de comprimento do elemento BD não excede 1,6mm.