Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 60
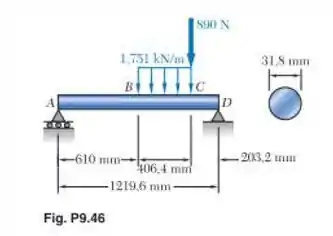
Para a viga e o carregamento indicados, determine o valor e localização da maior deflexão para baixo. Viga e carregamento do Problema 9.46.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos utilizar a equação que governa a linha elástica, dada por:
Então, nós precisamos da equação para o momento da viga, vamos determinar essa equação com o auxílio das funções de singularidade vistas nesse capítulo, depois disso conseguimos integrar a expressão acima para obter a equação para a inclinação. Integrando novamente conseguimos obter a equação para a deflexão, aí teremos tudo que precisamos para calcular o valor e a localização da maior deflexão para baixo. Então bora lá!
Passo 2
Beleza! Vamos começar desenhando o DCL para o sistema, onde teremos:
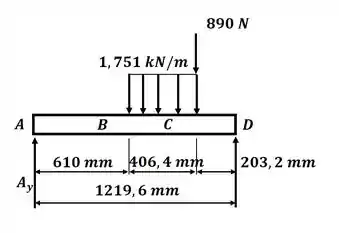
Beleza! Vamos aplicar o somatório de momento em relação ao ponto D para descobrir o valor da reação no ponto A, então teremos:
Agora vamos aproveitar e calcular o momento de inércia para a seção da viga. Como temos uma seção circular, o momento de inércia será:
Agora, como temos carregamento distribuído na viga que não vai até o final, precisamos de um carregamento equivalente que vá até o final da viga, para que possamos escrever as equações de singularidade. Então o carregamento equivalente será:
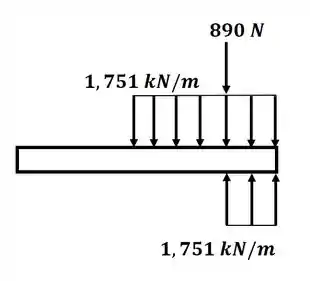
Agora, sabendo que a derivada da equação de cisalhamento corresponde ao oposto do carregamento, podemos escrever:
Passo 3
Agora, integrando essa expressão, teremos:
Nesse caso, a constante corresponde as forças localizadas aplicadas no sistema, como tomamos como referência do nosso sistema de coordenadas o ponto A, teremos a reação e a força de 890 N, então nossa constante será:
Então a equação para o cisalhamento se torna:
Agora, nós sabemos também que a derivada da equação momento corresponde ao cisalhamento, ou seja:
Então, substituindo a expressão encontrada para o cisalhamento nessa equação, temos:
Integrando essa expressão, teremos:
Nesse caso, a constante C representa os momentos localizados aplicados no sistema, no nosso caso não temos nenhum, então teremos:
Então nossa equação para o momento será:
Passo 4
Agora nós podemos utilizar a equação que governa o regime elástico descrita lá no passo 1 e substituir a equação obtida para o momento, então teremos:
Agora vamos integrar essa expressão, chegando em:
Agora nós vamos integrar a equação novamente para obter a equação da deflexão, então teremos:
Passo 5
Beleza! Agora, para encontrar o valor das constantes e , nós vamos usar as condições de contorno que temos nos apoios, onde sabemos que não há deflexão, ou seja:
Substituindo a primeira condição na equação para a deflexão encontrada no passo 4, teremos:
Agora, vamos utilizar a segunda condição de contorno para obter o valor de , então teremos:
Então, a nossa equação para a linha elástica será:
E a equação para a inclinação será:
Passo 6
Beleza! Agora, devido ao carregamento na viga estar concentrado somente na porção BC, é intuitivo notar que a maior deflexão estará nesse trecho. Nessa seção, a equação da inclinação e da deflexão se tornam:
Então, para descobrir a localização da maior deflexão, vamos igualar a equação da inclinação a zero, de onde teremos:
Como temos uma equação cúbica, vamos precisar da ajuda de uma calculadora, através dela, chegamos em uma posição da maior deflexão de:
Passo 7
Então agora nós vamos substituir a localização que encontramos no passo 6 na equação para a deflexão no nosso trecho BC, então teremos:
Prooonto! Terminamos mais um, valeeu!