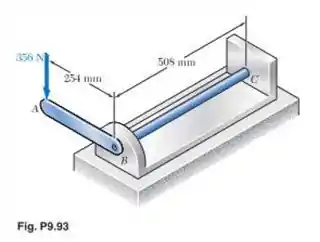
Uma barra BC de 22,2 mm de diâmetro é presa à alavanca AB e ao suporte fixo em C. A alavanca AB tem uma seção transversal uniforme com 9,5 mm de espessura e 25,4 mm de altura. Para o carregamento mostrado na figura, determine a deflexão no ponto A. Use E = 200 GPa e G = 77,2 MPa.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos utilizar o princípio da superposição para encontrar cada uma das deflexões e depois somar para encontrar uma expressão para a deflexão total em A, então vamos nessa!
Passo 2
Tá legal! Vamos começar esse exercício encontrando o momento de inércia da nossa barra, como temos uma seção circular, o momento de inércia será dado por:
Vamos precisar também do momento polar de inércia, que nada mais é do que o dobro do momento de inércia, ou seja:
Agora nós vamos encontrar o torque gerado em B devido a força aplicada no ponto A, então teremos:
Agora nós vamos encontrar a inclinação no ponto B devido ao torque aplicado nesse ponto. Sabemos que a deflexão nesse caso é dada por:
Substituindo os valores conhecidos, teremos:
Passo 3
Agora então podemos calcular a deflexão no ponto A devido a essa rotação, que será dada por:
Agora vamos encontrar a deflexão no ponto A devido a força localizada de 356 N. Nesse caso, temos uma força na ponta de uma haste engastada, para esse cenário, o caso 1 do apêndice D nos dá uma deflexão de:
Então, vamos calcular o momento de inércia para essa seção, sendo uma seção retangular, teremos:
Então, a deflexão no ponto A causada pela força de 356 N será:
E, então, a deflexão total no ponto A será dada por:
Shoow! Terminamos mais um, valeeu!