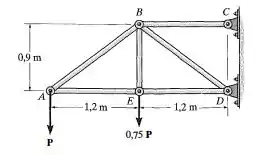
Cada uma das barras da treliça tem área de seção transversal de . Se a tensão normal média máxima em qualquer barra não pode ultrapassar , determine o valor máximo das cargas que podem ser aplicadas à treliça.
Passo 1
Fala aí galerinha do responde aí, tudo de boa? Bora pra mais uma questão.
O primeiro passo nesta questão é aplicar o método dos nós para saber as forças que atuam em cada barra. Logo, pegando primeiro o nó
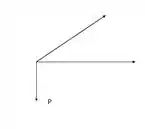
Pegando agora o nó
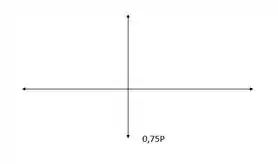
Pegando agora o nó
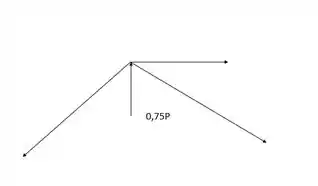
Antes de sair resolvendo esse monte de conta, pense comigo. Devemos escolher a maior força possível, que dará a tensão mais crítica. Olhe bem para a barra a força nela é a maior que tem, pois possui 3 somas em sua fórmula. Isso foi um pulo do gato, mas você pode fazer uma por uma e ver qual dará a maior força em função de P.
Passo 2
Agora, basta pegar a expressão do e achar o seu valor em função de
Como essa é a maior força, basta achar o valor de usando a relação da área com a tensão: