Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 115

A barra AB tem o movimento angular mostrado. Determine a aceleração do anel C nesse instante.

Passo 1

Começaremos o exercício analisando o sistema para descobrir os valores de velocidade angular e a distância do centro instantâneo de velocidade nula com relação a B com o auxílio do diagrama a seguir:

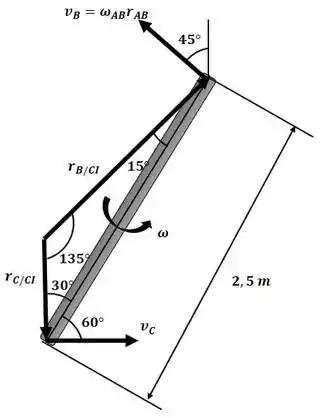
Através da lei dos senos, podemos escrever:

r B / C I s e n 30 ° = 2,5 s e n 150 ° →   r B / C I = 1,77   m    

Agora para a velocidade angylar da haste BC:

ω = v B r B / C I = ω A B r A B r B / C I = 5 ( 2 ) 1,77 → ω = 5,66   r a d / s

Passo 2

Agora iremos calcular o valor da aceleração normal em B com o auxílio do diagrama a seguir:

a B n = ω A B 2 r A B = 5 2 ( 2 ) → a B n = 50   m / s 2

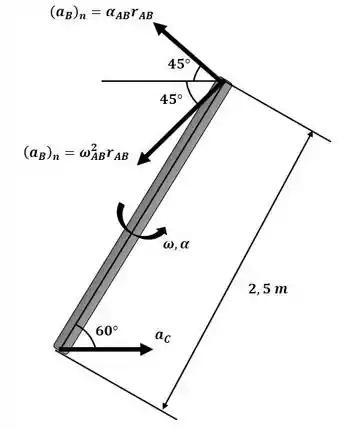
Passo 3

Agora podemos escrever a equação da aceleração em função das suas componentes, baseando-se no diagrama apresentado no passo 2:

a → C = a → B + a → C / B

+ →   a C = - 6 c o s 45 ° - 50 c o s 45 ° + 80 c o s 60 ° + α 2,5 c o s 30 °

a B t = 1,2 α

Essa será nossa equação 1.

+ ↑   0 = 6 s e n 45 ° - 50 s e n 45 ° + 80 s e n 60 ° - α 2,5 s e n 30 °

α = 30,5   r a d / s 2

Agora, substituindo esse valor na equação 1, temos:

  a C = - 6 c o s 45 ° - 50 c o s 45 ° + 80 c o s 60 ° + ( 30,5 ) 2,5 c o s 30 °

a C = 66,5   r a d / s 2

Resposta

a C = 66,5   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.149. No Problema 15.148, mostre que a trajetória de P é uma linha reta vertical quando r= R /2. Deduza expressões para a velocidade e aceleração de P correspondentes em qualquer instante t.
15.150. Duas barras rotativas estão conectadas por um bloco deslizante P. A barra presa em A gira com velocidade angular constante A. Para os dados fornecidos, determine para a posição mostrada nas fi
15.152. Duas barras rotativas estão conectadas por um bloco deslizante P. A velocidade v0 do bloco deslizante relativa à barra em que ele desliza tem velocidade constante e está orientada para fora. P
15.151. Duas barras rotativas estão conectadas por um bloco deslizante P. A barra presa em A gira com velocidade angular constante A. Para os dados fornecidos, determine para a posição mostrada nas fi
15.154. O pino P está preso ao colar mostrado na figura; o movimento do pino é guiado por um rasgo cortado na barra BD e pelo colar que desliza sobre a barra AE. Sabendo que, no instante considerado,