Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 113

No instante mostrado, o bloco deslizante B está se deslocando para a direita com a velocidade e aceleração mostradas. Determine a aceleração angular da roda nesse instante.

Passo 1

Começaremos o exercício analisando a velocidade do elo AB com o auxílio da figura a seguir:

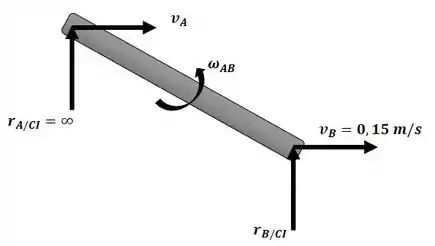
Usando o método do centro instantâneo de velocidade nula. Uma vez que v A e v B são paralelos, r A / C I = r B / C I = ∞ . Sendo assim:

ω A B = 0

E, por sua vez:

v A = v B = 0,15   m / s

Sendo assim, a velocidade angular da roda pode ser escrita como:

ω w = v A r O A = 0,15 0,125 → ω w = 1,2   r a d / s

Passo 2

Agora podemos aplicar a equação da aceleração para o esquema ilustrado no passo 1 para obter a aceleração no ponto A:

a → A = α w × r → O A - ω w 2 r → O A

a → A = ( - α w k → ) × 0,125 i → - 1 , 2 2 ( 0,125 j → )

a → A = 0,125 α w i → - 0,18 j →   m / s 2

Agora iremos aplicar a equação da aceleração para o diagrama completo a seguir:

a → B = a → A + α A B × r → B / A - ω A B 2 r → B / A

0,075 i → = 0,125 α w i → - 0,18 j → + α A B k → × 0,433 i → - 0,25 j → = 0

0,075 i → = 0,25 α A B + 0,125 α w i → + ( 0,433 α A B - 0,18 ) j →

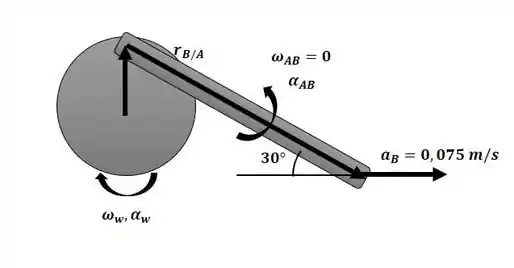
Passo 3

Igualando as componentes i e j da última equação do passo 2, temos:

0,075 = 0,25 α A B + 0,125 α w

0 = 0,433 α A B - 0,18 → α A B = 0,415   r a d / s 2

E substituindo esse valor na primeira equação:

0,075 = 0,25 ( 0,415 ) + 0,125 α w

α w = - 0,231   r a d / s 2     ↺

Resposta

α w = 0,231   r a d / s 2     ↺

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.153. Duas barras rotativas estão conectadas por um bloco deslizante P. A velocidade v0 do bloco deslizante relativa à barra em que ele desliza tem velocidade constante e está orientada para fora. P
15.154. O pino P está preso ao colar mostrado na figura; o movimento do pino é guiado por um rasgo cortado na barra BD e pelo colar que desliza sobre a barra AE. Sabendo que, no instante considerado,
Um disco com raio de 180m m gira à taxa constante ω 2 = 12r a d / s em relação ao braço C D , que por sua vez gira à taxa constante ω 1 = 8r a d / s em torno do eixo Y . Determine, no instante mostrad
Um disco com raio de 180m m gira à taxa constante ω 2 = 12r a d / s em relação ao braço C D , que por sua vez gira à taxa constante ω 1 = 8r a d / s em torno do eixo Y . Determine, no instante mostrad
Resolva o Problema 15.238 , considerando que θ = 40 ° .