Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 107

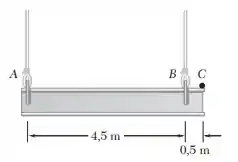
Uma viga de aço de 5 m está sendo baixada por meio de dois cabos que se desenrolam de guindastes à mesma velocidade. Assim que a viga se aproxima do solo, os operadores dos guindastes aplicam freios para desacelerar a descida. No instante considerado, a desaceleração do cabo preso em A é de 6 m/s², enquanto a do cabo preso em B é de 10 m/s². Determine (a) a aceleração angular da viga e (b) a aceleração do ponto C.

Passo 1

Vamos lá resolver mais essa. Os cabos que descem a viga de aço estão inicialmente na mesma velocidade, o que significa dizer que a velocidade angular da viga é zero. Quando os cabos sofrem uma aceleração desigual, temos a seguinte configuração dos vetores de aceleração:

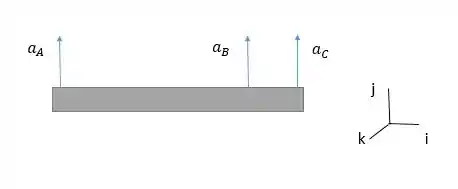
Assim, utilizaremos a seguinte relação:

a → B = a → A + a → B / A

Para obtermos a aceleração angular.

Passo 2

Vamos assumir que a aceleração angular tenha sentido anti-horário. Assim:

α → = α k →

Substituindo na relação do passo 1:

a → B = a → A + a → B / A

10 j → = 6 j → + α k → × 4,5 i → = 6 j → + 4,5 j →

α = 10 - 6 4,5 = 0,889   r a d / s   ( s e n t i d o   a n t i - h o r á r i o )

Passo 3

Podemos calcular a aceleração do ponto C por meio de:

a → C = a → A + a → C / A = a → A + α → × r → C / A

a → C = 6 j → + 0,889 k → × 5 i → = 6 j → + 4,445 j →

a → C = 10,45   m / s 2

Resposta

  1. 0,889 rad/s
  2. 10,45 m/s²
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A engrenagem A é mantida fixa, e o braço DE gira no sentido horário com uma velocidade angular ω D E = 6r a d / s e uma aceleração angular α D E = 3r a d / s 2 . Determine a aceleração angular da engr
O pino A no cotovelo AOD é guiado pelos frisos do cursor B, que desliza com uma velocidade constante v B de 0,9 m/s ao longo do eixo fixo durante um intervalo do movimento. Para a posição θ = 30 ° det
Se o centro O da roda do Prob. 5/199 possui uma velocidade constante de 150 mm/s para a esquerda, calcule a aceleração do cursor B para a posição θ = 0 .
Na posição mostrada a barra DC está girando no sentido anti-horário na taxa constante N = 2 r a d / s . Determine a velocidade angular ω e a aceleração angular α de EBO nesse instante.
O mecanismo da roda de Genebra é utilizado em um sistema de empacotamento para converter o movimento angular constante em movimento angular intermitente. A roda em estrela A realiza um sexto de uma re