Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 35
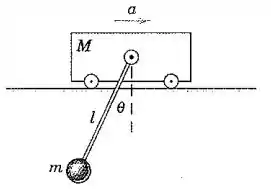
Uma barra de comprimento e massa desprezível conecta o carrinho de massa e a partícula de massa . Se o carrinho está submetido a uma aceleração constante para a direita, qual é o ângulo resultante em regime permanente que a barra livre faz com a vertical para girar? Determine a força (não apresentada) que deve ser aplicada ao carrinho para produzir a aceleração especificada.
Passo 1
Galera, a gente tem apenas duas forças agindo na partícula de massa : a força peso para baixo e a tração na barra, que puxa a partícula na direção do centro do carrinho. Como o ângulo permanece constante, as forças da vertical se equilibram, ou seja:
Porém, a partícula se move junto com o carrinho, indicando que tem a mesma aceleração para a direita. A única força que age para a direita da partícula é a componente da tração na barra, então ela é que causa essa aceleração:
Passo 2
Acabamos de obter duas equações que nos dizem o valor da tração . Vamos igualá-las entre si:
Assim, obtivemos o valor do ângulo . Para saber como é a força que deve ser aplicada no carrinho, basta notar que ela deve produzir uma aceleração para a direita no sistema carrinho-partícula de massa total , onde não atuam outras forças externas na direção .
Então, a força tem que ser aplicada necessariamente para a direita, e possuir o seguinte módulo, dado pela Segunda Lei de Newton:
Resposta
(para a direita)