Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 65
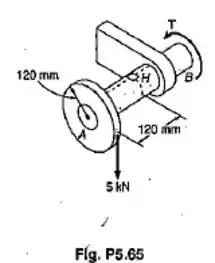
A força vertical 5 kN é aplicada ao aro, de um disco de raio igual a 120 mm, como mostrado. Sabendo-se que o eixo AB tem o diâmetro de 80 mm, determinar as tensões normal e de cisalhamento no ponto H.
Passo 1
Na seção que contém o ponto H nós temos
Temos sobre a barra sólia ainda que
Para área
Momento de inércia:
E para o J
Passo 2
Com essas informações spodemos comçar a calcular as tensões normal e de cisalhamento no ponto H
Resposta
Exercícios de Livros Relacionados
Escreva um código computacional que possa ser usado para determinar a tensão de cisalhamento máxima na viga que tem a seção transversal de mostrada na figura e é submetida a uma carga constante distri
A viga é composta por três peças de plástico coladas nas linhas de junção A e B. Se for submetida ao carregamento mostrado na figura, determine a força de cisalhamento vertical à qual resiste a aba su
A viga é composta por três peças de plástico coladas nas linhas de junção A e B. Se for submetida ao carregamento mostrado na figura, determine a tensão de cisalhamento desenvolvida nas juntas coladas
A viga tem seção transversal quadrada e está sujeita à força de cisalhamento V . Faça um rascunho da distribuição da tensão de cisalhamento na seção transversal e especifique a tensão de cisalhamento
Determine a variação da tensão de cisalhamento na seção transversal de um rebite oco. Qual é a tensão de cisalhamento máxima no rebite? Mostre também que, se r i → r o , então τ m á x = 2 V A á