Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 16

Uma barra delgada de 4 kg pode girar em um plano vertical em torno de um pivô em B. Uma mola de constante k = 400 N/m e comprimento indeformado de 150 mm é presa à barra como mostrado na figura. Sabendo que a barra é liberada do repouso na posição mostrada, determine sua velocidade angular após ela ter girado 90°.

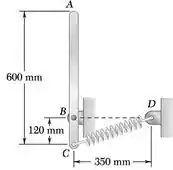
Passo 1

O enunciado pede que a gente determine sua velocidade angular após ela ter girado 90°.

Posição 1:

Mola:

x 1 = C D - 150   mm = 370 - 150 = 220   mm = 0.22   m

V e = 1 2 k x 1 2 = 1 2 400   N/m 0.22   m 2 = 9.68   J

Passo 2

Gravidade:

v G = W h = m g h = 4   kg 9.81   m/ s 2 0.18   m = 7.063   J

V 1 = V e + V g = 9.68   J + 7.063   J = 16.743   J

Energia cinética:

T 1 = 0

Passo 3

Posição 2:

Mola:

x 2 = 230   mm - 150   mm = 80   mm = 0.08   m

V e = 1 2 k x 2 2 = 1 2 400   N/m 0.08   m 2 = 1.28   J

Passo 4

Gravidade:

V g = W h = 0

V 2 = V e + V g = 1.28   J

Energia cinética:

v - 2 = r ω 2 = 0.18   m ω 2

I - = 1 12 m L 2 = 1 12 4   kg 0.6   m 2 = 0.12   kg ∙ m 2

T 2 = 1 2 m v - 2 2 + 1 2 I - ω 2 2 = 1 2 4   kg 0.18 ω 2 2 + 1 2 0.12 ω 2 2

T 2 = 0.1248 ω 2 2

Passo 5

Conservação da energia:

T 1 + V 1 = T 2 + V 2

0 + 16.743   J = 0.1248 ω 2 2 + 1.28   J

ω 2 2 = 123.9

ω 2 = 11.131   rad/s

Resposta

ω 2 = 11.13   rad/s  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o problema 18-127 assumindo que o meteorito choca no satélite em A em vez de B18.127 - Um satélite geoestacionário de 800 libras está girando com uma velocidade angular ω 0 = ( 1.5 r a d / s )
Um disco homogêneo de raio de 180 mm é soldado a uma haste AG de comprimento 360 mm e de massa desprezível, que é suportada por uma esfera e encaixe em A. O disco é liberado com uma taxa de spin ψ ˙ 0
Um cone sólido de 9 pol. Com uma base circular de raio de 3 pol. é suportado por uma junta esférica em A. Sabendo que o cone está girando em torno de seu eixo de simetria AB a uma taxa de 3000 rpm e q
Um disco homogêneo de raio de 180 mm é soldado a uma haste AG de 360 ​​mm de comprimento e de massa desprezível, que é conectada por uma manilha a uma vertical AB. A haste e o disco podem girar livrem
Resolva o problema de amostra 18.6 assumindo que o meteorito ataca p satélite em C com velocidade inicial v θ = ( 2000 m / s ) i