Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 106

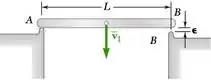
Uma barra delgada uniforme de comprimento L cai contra suportes rígidos em A e B. Como o suporte B está ligeiramente abaixo do suporte A, a barra bate no suporte A com uma velocidade v - 1 antes de bater em B. Admitindo um impacto perfeitamente elástico, tanto em A como em B, determine a velocidade angular da barra e a velocidade de seu centro de massa imediatamente após a barra ao (a) bater no suporte A, (b) bater no suporte B, (c) bater mais uma vez no suporte A.

Passo 1

O exercício pede que a gente determine a velocidade angular da barra e a velocidade de seu centro de massa imediatamente após a barra ao (a) bater no suporte A, (b) bater no suporte B, (c) bater mais uma vez no suporte A.

Momento de inércia é dada por:

I - = 1 12 m L 2

Passo 2

  1. Primeiro impacto em A.

    2. Condição do impacto:

    e = 1 :               v A 2 = v 1 ↑

    Cinemática:

    v - 2 = L 2 ω - v A 2 = L 2 ω - v 1

    Momentos sobre A:

    m v 1 L 2 + 0 = m v - 2 L 2 + I - ω 2 = m L 2 ω - v 1 L 2 + 1 12 m L 2 ω 2

    v - 2 = L 2 3 v 1 L - v 1 = 1 2 v 1

    v B 2 = L ω - v A 2 = 3 v 1 - v 1 = 2 v 1 ↓

    Passo 2

  2. Impacto em B.

    3. Condição do impacto:

    e = 1 :               v B 3 = 2 v 1 ↑

    Cinemática:

    v - 3 = v B 2 - L 2 ω = 2 v 1 - L 2 ω

    Momentos sobre B:

    - m v - 2 L 2 + I - ω 2 + 0 = m v - 3 L 2 - I - ω 3

    - m 1 2 v 1 L 2 + 1 12 m L 2 3 v 1 L + 0 = m 2 v 1 - L 2 ω 3 L 2 - 1 12 m L 2 ω 3

    v - 3 = 2 v 1 - L 2 3 v 1 L = 1 2 v 1

    v A 3 = L ω - v B 3 = 3 v 1 - 2 v 1 = v 1 ↓

    Passo 3

  3. Segundo impacto em A.

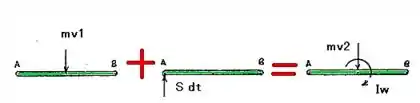
Condição do impacto:

e = 1 :               v A 4 = v 1 ↑

Cinemática:

v - 4 = v A 4 + L 2 ω 4 = v 1 + L 2 ω 4

Momentos sobre A:

m v - 3 L 2 + I - ω 3 + 0 = m v - 4 L 2 - I - ω 4

m 1 2 v 1 L 2 + 1 12 m L 2 3 v 1 L + 0 = m v 1 - L 2 ω 4 L 2 + 1 12 m L 2 ω 4

v - 4 + v 1 = 0

Resposta

ω 2 = 3 v 1 L

v - 2 = 1 2 v 1 ↓

ω 3 = 3 v 1 L

v - 3 = 1 2 v 1 ↑

ω 4 = 0

v - 4 = v 1 ↑

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que, no caso de amortecimento supercrucial (c c c ), um corpo liberado de uma posição arbitrária com uma velocidade inicial arbitrária não pode passar mais de uma vez pela sua posição de equilí
Um disco de 30 kg é fixado, com uma excentricidade e = 0,15 mm,ao ponto médio de um eixo vertical AB que gira com uma velocidadeangular ω ƒ ƒ constante. Sabendo que a constante de mola k para o movime
Mostre que, no caso de amortecimento supercrucial (c c c ), um corpo nunca passa pela sua posição de equilíbrio O (a) se ele é liberado sem velocidade inicial de uma posição arbitrária, ou (b) se ele
No caso de amortecimento subcrucial, os deslocamentos x 1 , x 2 , x 3 mostrados na Fig. 19.11 podem ser considerados iguais aos deslocamentos máximos. Mostre que a razão de dois deslocamentos máximoss
O bloco A pode se mover sem atrito na fenda como mostrado nafigura e sobre ele atuar uma força vertical periódica de intensidade P = P ms e nω ƒ t ƒ , onde ω ƒ = ƒ 2 rad /s e P m = 20 N. Uma mola de c