Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 57

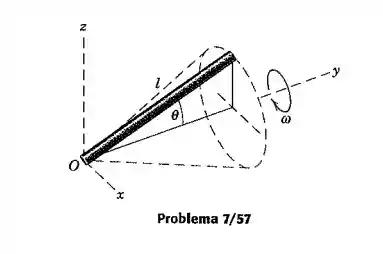
A barra esbelta de massa m e comprimento l gira em torno do eixo y como o elemento de um cone circular reto. Se a velocidade angular em torno do eixo y é ω , determine a expressão para a quantidade de movimento angular da barra em relação aos eixos x - y - z para a posição em particular mostrada.

Passo 1

Para resolvermos esse problema vamos precisar encontrar as componentes do tensor de inércia para a posição especificada, onde o ângulo θ será um ângulo arbitrário e importante para a questão. Após isso vamos utilizar a relação da quantidade de momento angular para finalizar o exercício.

Passo 2

Vamos começar analisando as informações que nos é dada. Pelo que é dito, sabemos que ω x = ω z = 0 e ω y = ω . Assim, temos que H = - I x y ⋅ i + I y y ⋅ j - I y z ⋅ k ⋅ ω . Precisamos então calcular 3 integrais que são as seguintes:

I x y = ∭ x ⋅ y ⋅ ρ ⋅ d V

I y z = ∭ y ⋅ z ⋅ ρ ⋅ d V

I y y = ∭ x 2 + z 2 ⋅ ρ ⋅ d V

Onde temos que x = 0 , y = s ⋅ cos ⁡ θ e z = s ⋅ sin ⁡ θ . Resolvendo então as integrais, chegamos que I x y = 0 , I y z = 1 3 ⋅ m ⋅ l 2 ⋅ sin ⁡ θ ⋅ cos ⁡ θ e I y y = 1 3 ⋅ m ⋅ l 2 ⋅ sin 2 ⁡ θ

Substituindo agora na equação da quantidade de movimento angular, ficamos com

H = i ⋅ 0 + j ⋅ 1 3 ⋅ m ⋅ l 2 ⋅ sin 2 ⁡ θ - k ⋅ 1 3 ⋅ m ⋅ l 2 ⋅ sin ⁡ θ ⋅ cos ⁡ θ

H = 1 3 ⋅ m ⋅ l 2 ⋅ ω ⋅ sin ⁡ θ ⋅ j ⋅ sin ⁡ θ - k ⋅ cos ⁡ θ

Resposta

H = 1 3 ⋅ m ⋅ l 2 ⋅ ω ⋅ sin ⁡ θ ⋅ j ⋅ sin ⁡ θ - k ⋅ cos ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6. O disco gira com uma velocidade angular de 15r a d / s em torno de seu eixo horizontal z , inicialmente na direção ( a ) e em seguida na direção ( b ) . O conjunto vira com a velocidade N = 10r a d
112. A estrutura principal de uma proposta de estação espacial consiste em cinco cascas esféricas conectadas por raios tubulares. O momento de inércia da estrutura em relação ao seu eixo geométrico A
108. A figura mostra um giroscópio montado com um eixo vertical e utilizado para estabilizar um navio hospital contra o balanço. O motor A gira o pinhão que produz a precessão do giroscópio pela rotaç
107. O pião de 12g de raio de giração em relação ao seu eixo de giro de 16m m está girando à taxa p = 3600r p m no sentido indicado, com seu eixo de giro fazendo um ângulo θ = 20 ° com a vertical. A d
121. A barra retangular está girando no espaço em torno de seu eixo longitudinal à taxa p = 200r p m . Se seu eixo oscila através de um ângulo total de 20 ° conforme mostrado, calcule o período τ da o