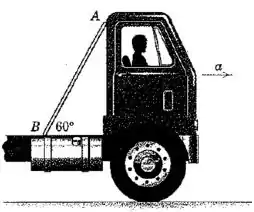
O coeficiente de atrito estático em ambas as extremidades da barra uniforme é igual a . Determine a aceleração horizontal máxima que o caminhão pode ter sem levar a barra a deslizar. (Sugestão: O problema pode ser resolvido usando apenas uma equação, uma equação de momentos. A localização do centro para os momentos pode ser determinada graficamente).
Passo 1
Nosso grande problema aqui é o seguinte: não conhecemos as forças de contato entre a barra e o caminhão em e .
Isso quer dizer que, para montar nossa equação de momentos, temos que escolher um ponto de referência que anule os momentos dessas duas forças. Podemos encontrar esse ponto graficamente:
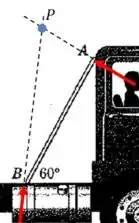
Passo 2
Beleza, então aquele vai ser nosso ponto de referência. O que fazemos a partir daqui? Agora escrevemos uma equação para os momentos restantes agindo sobre a barra:
Ou seja, a soma dos momentos é igual ao momento da força resultante.
Como a barra se move com aceleração , a força resultante é:
E o único momento que resta quando escolhemos aquele ponto de referência é o da força peso:
Ou seja:
Vamos representar essas distâncias no desenho:
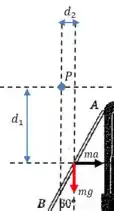
E agora nosso problema virou uma questão de geometria. Só precisamos calcular a razão entre as duas distâncias.
Passo 3
Vamos dar uma olhada no desenho para tentar calcular essa razão geometricamente. Começado por .
Podemos definir um ângulo que as forças de contato formam com a vertical/horizontal e usar ele pare encontrar . A partir daí o desenho fica um pouco complicado, por isso vamos distorcer algumas dimensões para facilitar a compreensão:
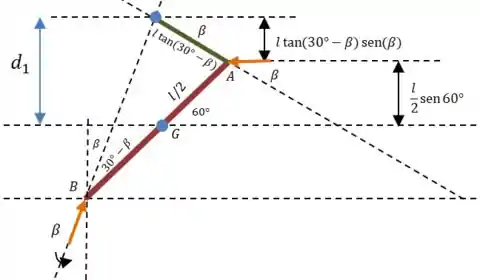
Olhe com calma para o desenho até que tudo faça sentido. Podemos ver que:
Agora vamos fazer a mesma coisa para .
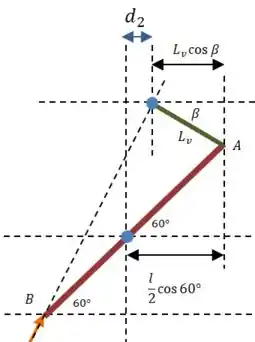
Olhando para o desenho de cima, lembre que o comprimento daquela linha verde é:
Então:
Passo 4
E o é o ângulo que as forças de contato em e formam com a horizontal/vertical,
Cada uma dessas forças de contato tem duas componentes perpendiculares uma a outra:
E então é:
Agora é só substituir os valores numéricos na nossa fórmula lá do passo 2:
Resposta
A aceleração horizontal máxima é .