Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.11 - Ex. 108
108. A figura mostra um giroscópio montado com um eixo vertical e utilizado para estabilizar um navio hospital contra o balanço. O motor gira o pinhão que produz a precessão do giroscópio pela rotação da grande engrenagem de precessão e do conjunto do rotor acoplado, em torno de um eixo transversal horizontal no navio. O rotor gira no interior de seu alojamento a uma velocidade no sentido horário de , quando visto de cima, e possui uma massa de com raio de giração de . Calcule o momento exercido sobre a estrutura do casco pelo giroscópio se o motor gira a engrenagem de precessão à taxa de . Em qual dos dois sentidos, (a) ou (b), o motor deve girar a fim de neutralizar o balanço do navio para bombordo.
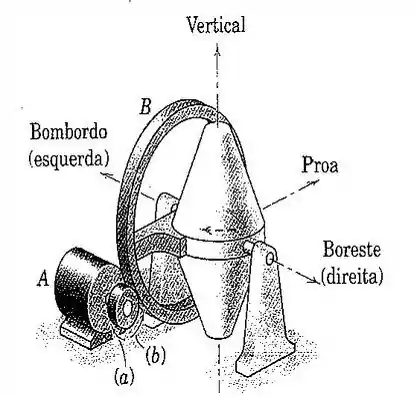
Passo 1
Inicialmente, vamos fazer o esboço das forças e momento que estão agindo no nosso sistema
Primeiro, vamos fazer o esboço dos momentos no pinhão e mecanismos ao seu redor:
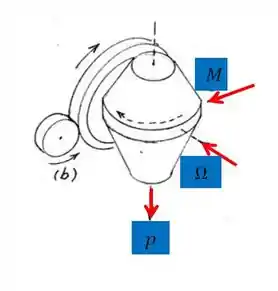
E depois, o esboço do momento resultante sobre a estrutura do casco, que é exercido pelo giroscópio:
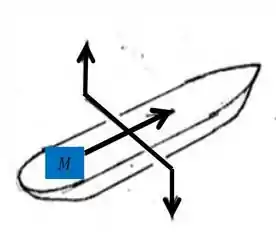
E conforme esperado, este momento vai se opor à direção do momento , gerado pelo giroscópio, que ilustramos na nossa primeira figura.
Passo 2
E o que nos resta, agora é calcular esse momento através da fórmula que já conhecemos:
Só que o momento de inércia é dado pela divisão do quadrado do raio de giração pela massa :
Substiuimos os valores numéricos e chegamos ao seguinte resultado:
E a direção desse momento é aquela que se opõe ao momento exercido pelo giroscópio. Logo, uma vez que o momento ocorre em sentido oposto ao do giroscópio, o motor deve girar na direção (b) a fim de neutralizar o balanço do navio para bombordo.