Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 238
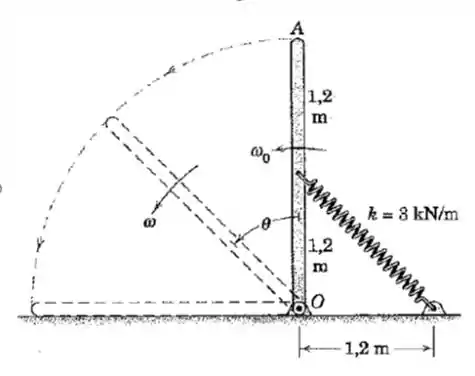
A barra esbelta de 30 kg tem uma velocidade angular inicial de ω=4 rad/s na posição vertical, onde a mola está sem deformação. Determine a velocidade angular mínima de ωmin alcançada pela barra e o ângulo θ correspondente. Encontre também a velocidade angular da barra quando atinge a superfície horizontal.
Passo 1
Definir a equação de conservação de energia:
AG = 1,2
Passo 2
Resolver equação e encontrar um:
Passo 3
Resolver equação e encontrar um:
Como:
Sugere-se utilização de software para obtenção dos resultados
Resposta
Assim ωmin = 0,910rad/s ; :
Exercícios de Livros Relacionados
Uma plataforma circular horizontal tem uma massa de 150 kg e um raio de giração k z = 2,4m em relação ao eizo z passando pelo seu centro O. A plataforma é livre para girar em torno do eixo z e está in
O corpo do satélite C tem uma massa de 200 kg e um raio de giração em relação ao eixo z de k z = 0,2m . Se o satélite gira em torno do eixo z com uma velocidade angular de 5 rev/s, quando os painéis s
Um homem de 75 kg salta para fora da plataorma circular com uma velocidade v m / p = 1,5m / s em relação à plataforma. Determine a velocidade angular da plataforma depois disso. Inicialmente o homem e
Duas crianças, A e B, cada uma tendo uma massa de 30 kg, estão sentadas na borda do carrossel que gira a ω = 2r a d / s . Excluindo as crianças, o carrossel tem uma massa de 180 kg e um raio de giraçã
Uma pessoa que passa através da porta giratória exerce uma força horizontal de 90N em um dos quatro painéis da porta e mantém o ângulo de 15° constante em relação a uma linha que é normal ao painel. S