Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 41

Duas crianças, A e B, cada uma tendo uma massa de 30 kg, estão sentadas na borda do carrossel que gira a ω = 2   r a d / s . Excluindo as crianças, o carrossel tem uma massa de 180 kg e um raio de giração k z = 0,6   m . Determine a velocidade angular do carrossel se A salta para fora horizontalmente na direção –n com uma velocidade de 2 m/s, medida em relação ao carrossel. Qual é a velocidade angular do carrossel se B, então, salta para fora horizontalmente na direção –t com uma velocidade de 2 m/s, medida em relação ao carrossel? Despreze o atrito e a dimensção de cada criança.

Passo 1

Começaremos o exercício calculando o momento de inércia do sistema nas suas três condições. Começaremos com o carrossel com as crianças ainda em cima:

I 1 z = 180 0,6 2 + 2 30 0,75 2

I 1 z = 98,55   k g . m 2

Agora para o carrossel quando a criança A pula do mesmo:

I 2 z = 180 0,6 2 + 30 0,75 2

I 2 z = 81,675   k g . m 2

Agora para o carrossel quando as duas crianças pularam:

I 3 z = 180 0,6 2 + 0

I 3 z = 64,8   k g . m 2

Passo 2

Agora iremos aplicar a conservação da quantidade de momento angular quando a criança A pula na direção –n com o auxílio da imagem a seguir:

H 2 z = H 3 z

I 2 z = I 3 z ω 3 - m B v B 0,75

81,675 2,413 = 64,8 ω 3 - 30 v B ( 0,75 )

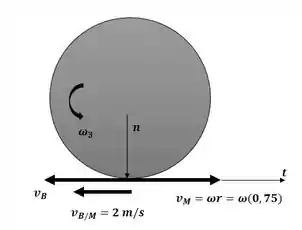
Essa será nossa equação número 1.

Passo 3

Agora iremos aplicar o conceito de velocidade relativa, com o auxílio da imagem do passo 2, para achar uma relação entre a velocidade da criança B e a velocidade angular do carrossel no instante 3:

v B = - v M + v B / M = - ω 3 0,75 + 2  

Agora, iremos substituir esse valor de v B na equação 1 obtida no passo 2:

81,675 2,413 = 64,8 ω 3 - 30 - ω 3 0,75 + 2   ( 0,75 )

ω 3 = 2,96   r a d / s

Resposta

ω 3 = 2,96   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois cilindros uniformes, cada um com peso W = 14 lb e raio r = 5 pol. são conectados por uma correia, conforme mostrado. Se o sistema é liberado do repouso quando t = 0, determine (a) a velocidade do
Um volante é rigidamente preso a um eixo de 1,5 pol. de raio que rola sem deslizar ao longo dos trilhos paralelos. Sabendo que após ser liberado do repouso o sistema atinge uma velocidade de 6 em 30 s
Uma roda de raio r e raio centroidal de giração k é liberada do repouso a inclinação mostrada no tempo t = 0. Supondo que a roda rola sem deslizar, determine (a) a velocidade de seu centro no tempo t,
Dois cilindros uniformes, cada um com peso W = 14 lb e raio r = 5 pol., são conectados por uma correia, conforme mostrado. Sabendo que no instante mostrado a velocidade angular do cilindro A é de 30 r
Considere uma laje rígida inicialmente em repouso e submetida a uma força impulsiva F contida no plano da laje. Definimos o centro de percussão P como o ponto de intersecção da linha de ação de F com