Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 35
Uma plataforma circular horizontal tem uma massa de 150 kg e um raio de giração em relação ao eizo z passando pelo seu centro O. A plataforma é livre para girar em torno do eixo z e está inicialmente em repouso. Um homem com uma massa de 75 kg começa a correr ao longo da borda em uma trajetória circular de raio 3 m. Se ele mantém uma velocidade de 1,2 m/s em relação à plataforma, determine a velocidade angular da plataforma. Despreze o atrito.
Passo 1
Começaremos o exercício expressando a velocidade absoluta do homem em função da velocidade da plataforma e de sua velocidade relativa em relação à mesma com o auxílio do esquema a seguir:
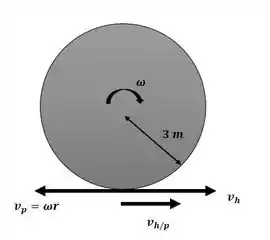
Passo 2
Com isso, podemos aplicar o conceito de conservação da quantidade de movimento angular para o sistema:
Resposta
Exercícios de Livros Relacionados
Dois discos de mesma espessura e mesmo material são presos a um eixo como mostrado na figura. O disco A de 3 kg tem um raio rA 100 mm e o disco B tem um raio r B 125 mm. Sabendo que a velocidade angul
No Problema 17.60, determine o tempo necessário para a velocidadedo volante ser reduzida a 40 rpm no sentido horário.
Dois discos de mesma espessura e mesmo material são presos a um eixo como mostrado na figura. O disco A de 4 kg tem um raio rA 100 mm e o disco B tem um raio r B 150 mm. Sabendo que o binário M de int
Mostre que a soma H A dos momentos sobre um Ponto A dos momentos das partículas de uma laje rígida em movimento plano é igual a I A ω , onde ω é a velocidade angular da laje no instante considerado e
O disco A de 7,5 lb tem raio rA = 6 pol. E está inicialmente em repouso. O disco B de 10 lb tem um raio = 8 pol. e uma velocidade angular ω 0 de 900 rpm quando ele é colocado em contato com o disco A.