Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 109
A barra esbelta uniforme de massa e comprimento , com pequenos roletes nas extremidades, é liberada a partir do repouso na posição mostrada, com o rolete inferior em contato com o plano horizontal. Determine a força normal sob o rolete inferior e aceleração angular da barra imediatamente após ser liberada.
Passo 1
Como queremos calcular a aceleração angular, é uma boa ideia usar a seguinte equação:
Só precisamos escolher algum ponto que seja conveniente, e para isso vamos precisar de um diagrama.
Em preto, vamos representar as forças que atuam sobre o corpo, assim poderemos escrever o somatório dos momentos .
Em azul vamos representar as forças resultantes agindo no centro de massa, assim poderemos escrever o outro somatório .
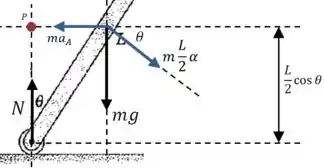
Passo 2
Se escolhermos o ponto , vamos eliminar os momentos de duas forças desconhecidas, o que facilitaria bastante nossa conta:
Então apenas a força peso contribuirá para o termo da esquerda. E o momento de inércia pode ser consultado em uma tabela:
Para o último termo, teremos apenas a contribuição da aceleração tangencial , lembre-se de que estamos fazendo o momento dessa força em relação ao ponto :
Então:
E com isso já podemos isolar a aceleração angular, que é a única variável desconhecida da equação. Começamos dividindo tudo por , e multiplicando por :
Passo 3
E agora, para encontrar a força normal, podemos usar a segunda lei de Newton na direção vertical:
As únicas forças que atuam nessa direção são o peso e a normal:
E apenas a aceleração tangencial tem uma componente nessa direção:
Então:
Vamos substituir a expressão que encontramos para :
Podemos simplificar um pouco se substituirmos aquele por uma fração:
Resposta
A força normal é e a aceleração angular .