Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 19.Problemas - Ex. 11

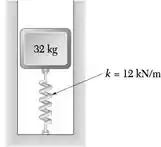
Um bloco de 32 kg ligado a uma mola de constante k = 12 kN/m pode se mover sem atrito em um rasgo como mostrado na figura. O bloco sofre um deslocamento inicial de 300 mm para baixo a partir da sua posição de equilíbrio e é liberado. Determine, 1,5 s depois de o bloco ter sido liberado (a) a distância total percorrida pelo bloco, (b) a aceleração do bloco.

Passo 1

O exercício pede que a gente encontre 1,5 s depois de o bloco ter sido liberado (a) a distância total percorrida pelo bloco, (b) a aceleração do bloco. Partiu?

  1. x = x m sin ⁡ ω n t + ϕ

    ω n = k m = 12 × 10 3   N/m 32   kg

    ω n = 19.365   rad/s

    τ n = 2 π ω n = 2 π 19.365

    τ n = 0.3245   s

    Passo 2

    Condições iniciais.

    x 0 = 0.3   m ,               x ˙ 0 = 0

    0.3 = x m sin ⁡ 0 + ϕ

    x ˙ 0 = 0 = x m ω m cos ⁡ 0 + ϕ

    ϕ = π 2

    x m = 0.3

    x t = 0.3 sin ⁡ 19.365 t + π 2 ,                 τ n = 0.3245   s

    x 1.5   s = 0.3 sin ⁡ 19.365 1.5 + π 2 = - 0.2147   m  

    x ˙ 1.5   s = 0.3 19.365 cos ⁡ 19.365 1.5 + π 2 = 4.057   m/s ↓  

    Passo 3

    Em um ciclo, o bloco viaja

    4 0.3   m = 1.2   m

    Para viajar 4 ciclos, leva

    4   cyc 0.3245   s/cyc = 1.2980   s

    Em  t  = 1,5 s. Assim, a distância total percorrida é

    4 1.2 + 0.6 + 0.3 - 0.2147 =   5,49

    Passo 4

x ¨ 1.5 = - 0.3 19.365 2 sin ⁡ 19.365 1.5 + π 2 = 80.5   m/ s 2 ↓

Resposta

a )  

5.49   m

b )   ⁡ 80.5   m/ s 2 ↓

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma série de pequenos componentes de máquina movidos por uma correia transportadora passa sobre uma polia esticadora de 150m m de raio. No instante mostrado na figura, a velocidade do ponto A é de 400
A lixadeira mostrada na figura está inicialmente em repouso. Se o tambor de acionamento B tem uma aceleração angular constante de 120r a d/ s 2 no sentido anti-horário, determine a intensidade da acel
Uma placa circular de raio 250m m mostrada na figura está inicialmente em repouso e tem a aceleração angular definida pela relação α = α 0 cos ⁡ ( π t / T ) . Sabendo que T = 1,5s e α 0 = 10r a d/ s 2
O anel C tem uma raio interno de 55 mm e um raio externo de 60 mm e é posicionado entre duas rodas A e B, cada uma com raio externo de 24 mm. Sabendo que a roda A gira com uma velocidade angular const
A velocidade nominal do tambor B da lixadeira mostrada na figura é de 2.400 rpm. Quando a lixadeira é desligada, observa-se que o tambor, então livre, alcança o repouso em 10 s. Admitindo-se um movime