Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 202
A barra esbelta uniforme de massa e comprimento tem velocidade angular nula quando a extremidade bate no chão sem nenhum movimento de retorno. Para um determinado valor da velocidade pouco antes do impacto, determine o ângulo mínimo para o qual a barra irá girar para a posição vertical após o impacto.
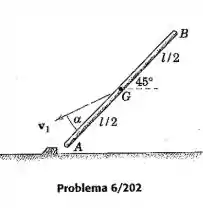
Passo 1
Pela conservação da quantidade de movimento angular, temos
Durante o impacto, ficamos com
Resolvendo para , obtemos
Passo 2
Após o impacto, a relação Trabalho-Energia é dada por
De onde tiramos que
Simplificando a equação anterior, temos
Resolvendo para , obtemos
Passo 3
Reparem que chegamos em duas equações distintas para . Igualando ambas, ficamos com
De onde tiramos que
Simplificando e resolvendo para , achamos
Resposta
Exercícios de Livros Relacionados
Solucione o Problema, considerando que o coeficiente de amortecimento do amortecedor é de c 300 N s/m.
No caso da vibração forçada de um sistema, determine o intervalo devalores do fator de amortecimento c / c c , para o qual o fator de ampliação sempre diminuirá quando a razão de frequência ω ƒ / ω n
Uma barra uniforme de massa m é suportada por um pino em A e uma mola de constante k em B e está ligada em D a um amortecedor de coeficiente de amortecimento c. Determine, em termos de m, k e c, para
Uma barra uniforme de 2 kg é suportada por um pino em O e poruma mola em A e está ligada a um amortecedor em B. Determine (a)a equação diferencial do movimento para pequenas oscilações, (b) oângulo qu
Um bloco A de 4 kg é solto de uma altura de 800 mm sobre um bloco B de 9 kg que está em repouso. O bloco B é suportado por uma mola de constante k = 1.500 N/m e está unido a um amortecedor de coeficie