Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 119

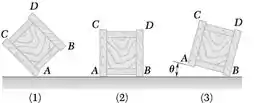
Um caixote quadrado uniformemente carregado é liberado do repouso com seu canto D diretamente acima de A; ele gira em torno de A até que seu canto B bata no chão, quando então passa a girar em torno de B. O chão é suficientemente áspero para impedir o deslizamento, e o impacto em B é perfeitamente plástico. Representando por ω 0 a velocidade angular do caixote imediatamente após B bater no chão, determine (a) a velocidade angular do caixote imediatamente antes de B bater no chão, (b) a fração da energia cinética do caixote perdida durante o impacto, (c) o ângulo em que o caixote irá girar após B bater no chão.

Passo 1

O enunciado pede que a gente determine (a) a velocidade angular do caixote imediatamente antes de B bater no chão, (b) a fração da energia cinética do caixote perdida durante o impacto, (c) o ângulo em que o caixote irá girar após B bater no chão.

Seja m a massa da caixa e c o comprimento de uma borda.

Momento de inércia.

I - = 1 12 m c 2 + c 2 = 1 6 m c 2

Passo 2

Cinemática:

v - 0 = r G / A ω 0 = 1 2 2 ω 0

v - = r G / B ω = 1 2 2 c ω

Momentos sobre B:

I - ω 0 + 0 = I - ω + r G / B m v -

1 6 m c 2 ω 0 + 0 = 1 6 m c 2 ω + 1 2 2 c m 1 2 2 c ω = 2 3 m c 2 ω

Passo 3

  1. Resolvendo para ω ,

    2. Energia cinética.

    Antes do impacto:

    T 1 = 1 2 I - ω 0 2 + 1 2 m v - 0 2 = 1 2 1 6 m c 2 ω 0 2 + 1 2 m 1 2 2 c ω 0 2 = 1 3 m c 2 ω 0 2

    Depois do impacto:

    T 2 = 1 2 I - ω 2 + 1 2 m v - 2 = 1 2 1 6 m c 2 ω 2 + 1 2 m 1 2 2 c ω 2 = 1 3 m c 2 ω 2 = 1 3 m c 2 1 4 ω 0 2 = 1 48 m c 2 ω 0

    Passo 2

  2. Fração de energia perdida:

    3. T 1 - T 2 T 1 = 1 3 - 1 48 1 3 = 1 - 1 16

    Conservação de energia durante a queda.

    T 0 + V 0 = T 1 + V 1

    Conservação de energia durante a subida.

    T 0 + V 0 = T 1 + V 1

    Condições:

    T 0 = 0 ,             T 3 = 0               T 2 = 1 16 T 1

    V 0 = m g 1 2 2 c             V 1 = V 2 = m g 1 2 c                 V 3 = m g h 3

    Da Equação (1),

    T 1 = V 0 - V 1 = 1 2 2 - 1 m g c

    Da Equação (2),

    T 2 = V 3 - V 2 = m g h 3 - 1 2 m g c

    h 3 - 1 2 c 1 2 2 - 1 = 1 16                 h 3 = 1 2 + 1 16 2 - 1 c

    Passo 3

  3. Da geometria,

h 3 = 1 2 2 c sin ⁡ θ + 45 °

Equacionando as duas expressões para h3,

sin ⁡ 45 ° + θ = 1 2 + 1 16 2 - 1 1 2 2

45 ° + θ = 46.503 ° = 1.50 °

Resposta

a )   ω = 1 4 ω 0  

b )   15 16

c )   θ = 1.50 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bombeiro de 75k g está segurando uma mangueira que tem um diâmetro do bocal de 25m m e o diâmetro do corpo de 50m m . Se a velocidade da água na descarga é 18m / s , determine as forças normal e de
O carro de 75k g , de uma atração de parque de diversões, está conectado a uma lança telescópica giratória. Quando r = 4,5m , o carro move-se em uma trajetória horizontal circular a uma velocidade de
Um satélite de massa 700k g é lançado em uma trajetória de voo livre em torno da Terra a uma velocidade inicial v A = 10k m / s , quando a distância do centro da Terra é r A = 15M m . Se o ângulo de l
No instante que r = 1,5m , ao disco de 5k g é dada uma velocidade v = 5 m / s , perpendicular à corda elástica. Determine a velocidade do disco e a taxa de encurtamento da corda elástica no instante r
A bola de 2k g gira em torno de uma trajetória circular de 0,5m de diâmetro com velocidade constante. Se o comprimento da corda é encurtado de l = 1m até l ' = 0,5m , puxando-se a corda através do tub