Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 220
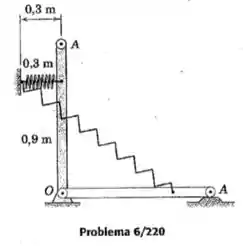
A barra esbelta uniforme tem uma massa de e é liberada a partir do repouso na posição próxima da vertical mostrada, onde a mola com rigidez de está sem deformação. Calcule a velocidade com que a extremidade atinge a superfície horizontal.
Passo 1
Bom, vamos utilizar a lei de conservação de energia, mas primeiro, vamos escrever cada uma das equações de cada energia envolvida no processo. Vamos começar pela energia cinética, a barra parte do repouso, então a energia cinética inicial é zero, e a final será dada pela rotação da barra em torno do eixo O, a equação será:
A energia potencial elástica da mola será zero na posição inicial da barra, pois não há deformação, sobrando apenas a energia potencial elástica final que é dada por:
E por fim, a energia potencial gravitacional será zero na posição final do sistema já que colocaremos a altura da barra no final como a altura zero no referencial, sobrando apenas a inicial, que será dada por:
Relacionando as três:
Passo 2
Precisamos determinar o momento de inercia em relação ao ponto O, pelo valor tabelado para a barra com eixo passando em uma extremidade:
E reescrevendo em termos da velocidade linear do ponto A:
Onde é o comprimento da barra.
Também precisamos determinar o valor da deformação x da mola, para isso, calculamos a hipotenusa d formada pela barra entre o antes e o depois do movimento, e depois subtraímos o comprimento da mola:
E então x será:
E por último, a altura h do centro de massa antes do movimento será a metade do comprimento da barra
Passo 3
Nossa lei da conservação então fica:
Isolando :
Substituindo valores: