Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 67

A caixa A de 50   k g é liberada do repouso sobre a rampa lisa. Depois de deslizar pela rampa atinge a caixa B de 100   k g , que está em repouso contra uma mola de rigidez k = 10   k N / m . Se o coeficiente de restituição entre as caixas é e = 0,5 , determine suas velocidades logo após o impacto. Além disso, qual é a compressão máxima da mola? A mola está originalmente não deformada.

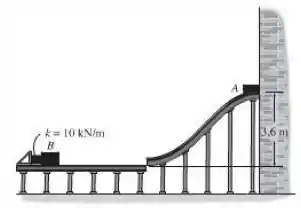
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Aplicando conservação de energia, temos:

T A 1 + V A 1 = T A 2 + V A 2

0 + 50 9,81 3,6 = 1 2 5 0 v A 2 2 + 0

v A 2 = 8,4   m / s

Aplicando conservação de quantidade de movimento:

50 8,4 + 0 = 50 v A 3 + 100 v B 3

v A 3 + 2 v B 3 = 8,4

O coeficiente de restituição é dado por:

e = v B 3 - v A 3 v A 2 - v B 2

0,5 = v B 3 - v A 3 8,4 - 0

v B 3 - v A 3 = 4,2

Logo:

v B 3 = 4,2   m / s

v A 3 = 0

Por conservação de energia podemos encontrar a compressão máxima da mola.

T B 3 + V B 3 = T B 4 + V B 4

1 2 100 4,2 2 + 0 = 0 + 1 2 10000 s m á x 2

s m á x = 0,42   m

Resposta

v B 3 = 4,2   m / s

v A 3 = 0

s m á x = 0,42   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula de massa m é lançada do ponto A com uma velocidade inicial v0 perpendicular à linha OA e se movimenta sob a ação de uma força central F ao longo de uma trajetória semicircular de diâmetr
Uma partícula de massa m é lançada do ponto A com uma velocidade inicial v0 perpendicular à linha OA e se movimenta sob a ação de uma força central F ao longo de uma trajetória semicircular de diâmetr
A haste 0A gira cerca de 0 em um plano horizontal. O movimento do colar B de 300 g é definido pelas relações r = 300 + 100 c o s ⁡ ( 0.5 π t ) e θ = π t 2 - 3 t , onde r é expresso em milímetros, t em
Para o movimento definido no Problema 12.66, determine os componentes radial e transversal da força exercida no colar quando t = 1,5 s.12. 66 - A haste 0A gira cerca de 0 em um plano horizontal. O mov
Um colar B de massa m desliza no braço sem fricção AA '. O braço está preso ao tambor D e gira cerca de 0 em um plano horizontal na taxa θ ˙ = c t , onde c é uma constante. Conforme o conjunto braço-t