Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 201

Uma esfera sólida homogênea de raio r está em repouso no fundo de um tanque contendo um líquido de densidade ρ l , que é maior que a densidade ρ s do esfera. Conforme o tanque é preenchido, uma profundidade h é alcançada emqual a esfera começa a flutuar. Determine a expressão para a densidade ρ s da esfera.

Passo 1

E ai gurizada tudo belezinha???

A esfera flutua quando se torna flutuante de forma neutra. A massa da esfera será igual à massa do líquido deslocado. m s = m d

4 3   π   r 3 ρ s = ρ 1 ×     volume de líquido deslocado

Passo 2

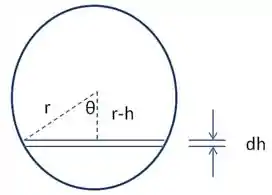
Colete o volume do líquido deslocado somando as fatias da esfera de largura dh da base og do tanque. Cada fatia tem raio.

r sin ⁡ θ = r r 2 - ( r - h ) ² r = r 2 - ( r - h ) ²

4 3   π   r 3 ρ s = ρ l ∫ 0 h π r 2 - r - h 2 2 d h = ρ l ∫ 0 h π   r 2 - ( r - h ) ²   d h

4 3     r 3 ρ s = ρ l ∫ 0 h     2   r   h - h ²   d h

4 3     r 3 ρ s = ρ l       r   h 2 - h ³ 3

ρ s = ρ l   3   h ³ 4   r ² = h ³ 4   r ³ = ρ l h 2   r ² 3 - h r

Agora sim, terminamos

Resposta

ρ s = ρ l h 2   r ² 3 - h r  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um arame homogêneo é dobrado na forma mostrada na forma a seguir. Determine por integração direta a coordenada x de seu centroide.
Determine o volume e a área da superfície do elo de corrente mostrado na figura, que é feito de uma barra de 6m m de diâmetro, se R = 10m m e L = 30m m .
Determine por integração direta os centroides das áreas a seguir.v
Determine o volume e a área da superfície do sólido obtido pela rotação da área da área do problema erm torno de ( a ) da linha y = 60 m m , ( b ) do eixo y .
Determine por integração direta os centroides das áreas a seguir.