Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 13

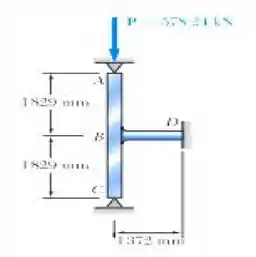
A barra BD feita de aço (   E = 200   G P a ) é utilizada para contenção lateral da haste comprimida ABC. O máximo esforço que se desenvolve em BD é igual a 0,02P. Se a tensão não deve exceder 124,1 MPa e a máxima mudança de comprimento da barra BD não pode exceder 0,001 vez o comprimento de ABC, determine o menor diâmetro possível de ser utilizado para o membro BD.

Passo 1

Fala aí galera tudo belezinha?

F B D = 0,02   P = 0,02   x   5 78,24 =   11 , 56   k N = 11,56 × 10 3   N

Considerando a tensão: σ = 124,1   M P a = 124,1     x   10 6   P a , podemos determinar a área a partir da equação da tensão... σ = F B D A           ∴       A = F E D σ = 11,56 × 10 3 124,1   ×   10 6 = 9,32 × 10 - 5 m ²

Considerando a deformação: δ = 0,001   x   3,658 = 3,658 × 10 - 3   m δ = F B D L B D A E       ∴       A = F B D L B D E δ = 11,56 × 10 3   x   ( 1,372 ) 200   x   10 9   x   ( 3,658 × 10 - 3 ) = 2,17 × 10 - 5   m 2

Área maior governa: A = 9,32 × 10 - 5 m ² A = π 4 d 2         ∴       d = 4 A π = 4   x   ( 9,32 × 10 - 5 ) π

d = 0,0109   m

d = 10,9   m m

Resposta

d = 10,9   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A roseta de deformação a 60° está montada sobre uma viga. As seguintes leituras foram obtidas para cada extensômero: ∈ a = - 780 × 10 - 6 ;∈ b = 400 × 10 - 6 e ∈ c = 500 × 10 - 6 . Determine (a) as de
A roseta de deformação a 45 ° está montada sobre um eixo de aço. As seguintes leituras foram obtidas em cada extensômetro: ϵ a = 800 ( 10 - 6 ) , ϵ b = 520 ( 10 - 6 ) , ϵ c = - 450 ( 10 - 6 ) . Determ
A roseta de deformação a 45° está montada próxima ao dente da ferramenta. As seguintes leituras foram obtidas para cada extensômero: ∈ a = 800 × 10 - 6 ;∈ b = 520 × 10 - 6 e ∈ c = - 450 × 10 - 6 . Det
Considere o caso geral de deformação plana na qual ϵ x ,ϵ yeγ x y são conhecidas. Escreva um código computacional que possa ser usado para determinar a deformação normal e a deformação por cisalhament
Considere a orientação geral dos três extensômetros em um único ponto como mostra a figura. Escreva um código computacional que possa ser usado para determinar as deformações principais no plano e a d