Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 67
A montagem consiste de duas barras de 4 kg que estão conectadas por pinos aos dois discos de 5 kg. Se as barras são liberadas do repouso quando = 60°, determine suas velocidades angulares no instante = 30°. Suponha que os discos rolam sem deslizar.
Passo 1
Iremos considerar a aceleração da gravidade
Antes de aplicar a equação da conservação da energia mecânica, é importante notar que as barras terão a mesma velocidade angular, uma vez que o dispositivo é simétrico e os discos possuem o mesmo tamanho, logo:
Passo 2
Nesse caso, diferentemente do problema 18.66, como as barras ainda não estarão totalmente esticadas na posição final, teremos componentes de velocidade linear das barras e dos discos. Sendo assim, a velocidade linear da barra AB no seu centro de massa é dada por:
A velocidade angular do disco A é dada por:
Onde é a velocidade linear do disco A. No entanto, sabemos que essa velocidade é dada por:
Substituindo essa expressão na equação anterior:
Obtemos a relação entre a velocidade angular do disco A e da barra AB.
Passo 3
Com isso e com o auxílios das duas figuras representando a condição inicial:
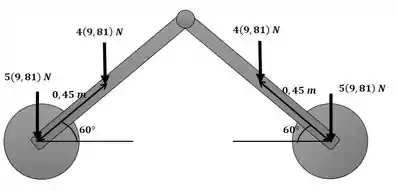
E a condição final:
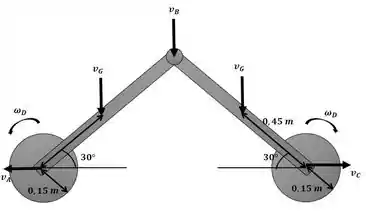
Podemos agora aplicar a equação da conservação da energia mecânica para encontrar a velocidade angular das barras:
Resolvendo a equação para :
E, como as velocidades angulares são iguais (conforme visto no passo 1):