Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 140

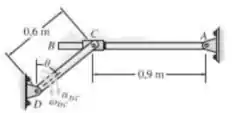
No instante θ = 45 ° , o membro DC tem uma velocidade angular ω D C = 4   r a d / s e uma aceleração angular α D C = 2   r a d / s 2 . Determine a velocidade angular e a aceleração angular da barra AB nesse instante. O anel em C está conectado por pino a DC e desliza livremente ao longo de AB.

Passo 1

Antes de iniciarmos a resolução do exercício, vamos pegar as constantes que o enunciado nos fornece. Então,

v A = a A = 0 ω C D = - 4 k   r a d / s α D C = 2 k   r a d / s 2

v A / O x y z = v C / A r e l i   m / s a C / A x y z = a C / A r e l i   m / s 2 r C / A = - 0,9 i   m

Agora que já possuímos os dados do enunciado, vamos calcular o valor de v C . Para nos ajudar, iremos tomar como base a figura abaixo:

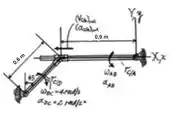
v C =   ω C D × r C / D = - 4 k × ( 0,6 . sen ⁡ 45 ° i + 0,6 . cos ⁡ 45 ° j ) = 1,6971 i - 1,6971 j   m / s

Bom, calculamos v C , agora temos condições de calcular v C / A x y z e ω A B . Para que a gente consiga chegar nesses dois resultados, vamos utilizar a fórmula da velocidade relativa.

v c = v a + Ω × r C / A + v C / A x y z

Vamos substituir os valores que conhecemos na equação acima.

1,6971 i - 1,6971 j = 0 + ω A B k × - 0,9 i + v C / A x y z i

1,6971 i - 1,6791 j = v C / A x y z i - 0,9 . ω A B j

Como iremos resolver a equação acima? Fácil! Como as coordenadas têm que ser iguais, então:

1,6971 i = v C / A x y z i

- 1,6971 j = - 0,9 . ω A B j

Resolvendo as igualdades acima, chegaremos em:

v C / A x y z = 1,6971   m / s e ω A B = 1,8857   r a d / s

Passo 2

Para encontrarmos a aceleração, iremos utilizar a fórmula daaceleração relativa abaixo:

a C = a A + Ω ˙ × r C / A + Ω × Ω × r C / A + 2 . Ω × v C / A x y z + a C / A x y z

Mas se observarmos a equação acima, vamos perceber que não temos o valor de a C , mas isso será fácil de resolver. Podemos calcular a C como:

a C = α C D × r C / D - ω C D 2 . r C / D

Substituindo os valores:

a C = - 2 k × ( 0,6 . sen ⁡ 45 ° i + 0,6 . cos ⁡ 45 ° j ) - 4 2 . ( 0,6 . sen ⁡ 45 ° i + 0,6 . cos ⁡ 45 ° j ) = - 5,9397 i - 7,6367 j   m / s 2

Passo 3

Agora que conseguimos encontrar o valor de a C , vamos voltar e encontrar o α A B . Para isso, utilizaremos a fórmula abaixo:

a C = a A + Ω ˙ × r C / A + Ω × Ω × r C / A + 2 . Ω × v C / A x y z + a C / A x y z

Substituindo os valores conhecidos:

- 5,9397 i - 7,6367 j = 0 + ( α A B k ) × ( - 0,9 i ) + ( 1,8857 k ) × [ 1,8857 k × ( - 0,9 i ) ] + 2 . ( 1,8857 k ) × ( 1,6871 i ) + a C / A x y z i

Resolvendo a parte da direita, iremos encontrar:

- 5,9397 i - 7,6367 j = - 0,9 . α A B j + 3,2002 i + 6,3627 j + a C / A x y z i

Assim como feito no Passo 1, vamor igualar as coordenadas.

a C / A x y z = - 9,14   m / s 2

α A B = 15,55   r a d / s 2

Resposta

ω A B = 1,8857   r a d / s

α A B = 15,55   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cilindro hidráulico D se estende com uma velocidade v B = 1,2m / s e uma aceleração a B = 0,45m / s 2 . Determine a aceleração de C no instante mostrado.
O bloco deslizante se desloca com uma velocidade v B = 1,5m / s e uma aceleração a B = 0,9m / s 2 . Determine a aceleração angular da barra AB no instante mostrado.
O bloco deslizante se desloca com uma velocidade v B = 1,5m / s e uma aceleração a B = 0,9m / s 2 . Determine a aceleração de A no instante mostrado.
A manivela AB gira com uma velocidade angular ω A B = 6r a d / s e uma aceleração angular α A B = 2r a d / s 2 . Determine a aceleração de C e a aceleração angular de BC no instante mostrado.
A polia A gira com a velocidade angular e aceleração angular mostradas. Determine a aceleração angular do bloco E no instante mostrado.