Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 62

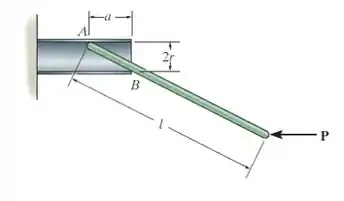
A barra fina de comprimento l é sustentada pelo tubo liso. Determine a distância a necessária para o equilíbrio se a cara aplicada é P .

Passo 1

Em toda questão de mecânica geral nós sempre devemos desenhar o diagrama de corpo livre da situação para entendermos quais são as forças e componentes envolvidas. A distância entre os pontos A e B pode ser facilmente encontrada através do teorema de pitágoras, resultando em a 2 + 4 r 2 . A altura do ponto A para onde está sendo aplicada a força P é calculada através de uma semelhança de triângulos, que resulta em 2 r a 2 + 4 r 2 l . Para essa questão, temos o seguinte diagrama:

Passo 2

O jeito mais prático de encontrarmos quando vale a força P é somando as forças horiontais. Para a situação de equilíbrio do sistema, o somatório de forças na horizontal é igual a zero. Assumindo que o sentido para a direita é positivo, temos:

2 r a 2 + 4 r 2 N B - P = 0

P = 2 r a 2 + 4 r 2 N B

Passo 3

Vamos agora calcular o momento em relação ao ponto A . Para a situação de equilíbrio do sistema, o somatório do momento em relação a um ponto é igual a zero. Assumindo o sentido anti-horário como positivo, temos:

- P 2 r a 2 + 4 r 2 l + N B 4 r 2 + a 2 = 0

4 r 2 4 r 2 + a 2 = a 2 + 4 r 2

4 r 2 = a 2 + 4 r 2 3 2

4 r 2 2 3 = a 2 + 4 r 2

a 2 = 4 r 2 2 3 - 4 r 2

a = 4 r 2 2 3 - 4 r 2

Resposta

A distância é:

a = 4 r 2 2 3 - 4 r 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as reações no elemento em “L” que é apoiado por uma superfície lisa em B e por uma luva em A , que está fixa ao elemento e livre para deslizar pela alça inclinada presa à parede.
Determine as reações que atuam sobre o elemento uniforme liso, que tem massa de 20 kg.
A lança apoia duas cargas verticais. Desconsidere o tamanho dos colares em D e B e a espessura da lança, e calcule as componentes horizontal e vertical da força no pino A e a força no cabo C B . Consi
As dimensões de um guindaste, que é fabricado pela Basick Co., são dadas na figura. Se o guindaste tem massa de 800 kg e centro de massa em G , e a força máxima prevista para sua extremidade é F = 15k
O anteparo A D está sujeito às pressões da água e do aterramento de contenção. Supondo que A D esteja conectado ao solo em A por um pino, determine as reações horizontal e vertical nesse ponto e també