Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 103
9.103 Determine a altura à qual o líquido deve ser vertido no copo de papel cônico de modo que atinja a metade da área de superfície no interior do copo.
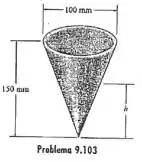
Passo 1
Para gerarmos a superfície do copo inteiro devemos fazer a revolução do segmento de reta a seguir:
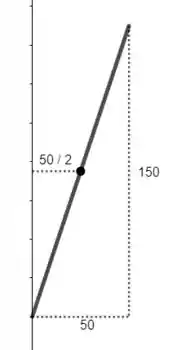
Essa área deve ser duas vezes maior que a gerada pela revolução dessa reta:
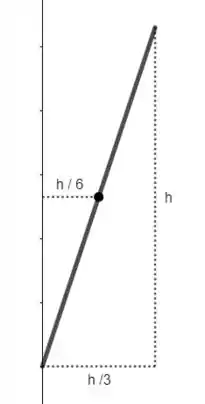
Podemos escrever essa relação dessa forma:
A fórmula para determinar a área superficial é:
Onde é o ângulo de revolução em radianos, nesse caso . Então a equação vai ficar assim:
Passo 2
é a distância perpendicular do eixo de revolução ao centroide da curva de geração.
O centroide de uma segmento de reta fica sempre no seu centro, então é fica fácil de calcularmos:
e
E é o comprimento da curva de geração, podemos usar pitagoras para descobrir:
O vai ser calculado em função de , também por pitagoras:
Passo 3
Agora só multiplicar aplicar na fórmula: