Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 33
Uma força é aplicada perpendicularmente ao cabo pé de cabra, conforme a figura. Se o coeficiente de atrito estático entre a barra e a madeira for , determine a força normal de unha em na tábua superior. Assuma que a susperfície em seja lisa.
Passo 1
O problema pede que descubra a força normal em .
Beleza, vamos começar fazendo um diagraminha de corpo livre:
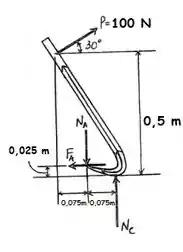
A gente consegue encontrar a força , pois as únicas forças na horizontal são e , e a gente conhece , logo fica assim:
Passo 2
E a gente pode analisar o momento tendo como eixo de rotação o ponto , então, vamos lá:
Passo 3
Calma, tá quase acabando, agora a gente analisar as forças na vertical:
Resposta
Exercícios de Livros Relacionados
Considerando apenas valores de θ menores que 90°, determine o menor valor de θ solicitado para o qual o movimento do bloco para a direita é iminente quando ( a ) W = 340 N, ( b ) W = 450 N.
Os coeficientes de atrito entre o bloco e o trilho são μ s = 0,3 e μ k = 0,25 . Sabendo que θ = 65 ° , determine o menor valor da força P necessária ( a ) para iniciar o movimento do bloco sobre o tri
O bloco de 360 N está ligado à articulação AB e repousa sobre uma esteira em movimento. Sabendo que μ s = 0,25 e μ k = 0,2 determine a intensidade da força horizontal P que pode ser aplicada na esteir
Três pacotes de 4 kg, A, B e C são colocados em uma esteira transportadora que está em repouso. Entre a esteira e os pacotes A e C, os coeficientes de atrito são μ s = 0,3 e μ k = 0,2 ; entre o pacote
O cilindro mostrado na figura tem peso W e raio r. Expresse, em termos de W e r, a intensidae do maior binário M que pode ser aplicado ao cilindro para que ele não gire, considerando que o coeficiente